Força e Torque sobre uma Espira
Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.
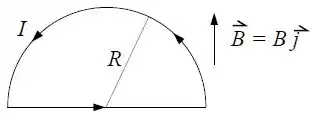
Determine o vetor torque exercido por sobre o circuito.
Passo 1
Determine o vetor torque exercido por sobre o circuito.
Por definição, o torque sobre uma espira é dada por:
Onde é o momento dipolar elétrico, definidor por:
Onde é o vetor cujo módulo é igual à área que do circuito, direção perpendicular ao plano do circuito e sentido dado pela regra da mão direita.
Como a corrente flui no sentido anti-horário, pela regra da mão direita, teremos:
Logo:
E, finalmente, o torque será dado por:
Resposta
Exercícios de Livros Relacionados
Uma esfera uniforme, sólida, uniformemente carregada, de raio R , tem uma densidade volumétrica de carga ρ . A esfera gira em torno de um eixo que passa pelo seu centro com rapidez angular ω . Determi
Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo 2,30 A · m 2 . (b) Determine o valor máximo do torque a que a bo
Uma espira circular com 8,0 cm de raio é percorrida por uma corrente de 0,20 A . Um vetor de comprimento unitário, paralelo ao momento dipolar μ → da espira, é dado por 0,60 i ^ – 0,80 j ^ . (Esse vet
Na Fig. 28-50a, duas espiras concêntricas, situadas no mesmo plano, são percorridas por correntes em sentidos contrários. A corrente i 1 na bobina 1 é fixa e a corrente i 2 na bobina 2 é variável. A F
A bobina da Fig. 28-49 conduz uma corrente i = 2,00 A no sentido indicado, é paralela ao plano x z , possui 3,00 espiras, tem uma área de 4,00 × 10 - 3 m 2 e está submetida a um campo magnético unifor