Considere um fio de comprimento por onde passa uma corrente colocado ao longo do eixo , conforme a figura.
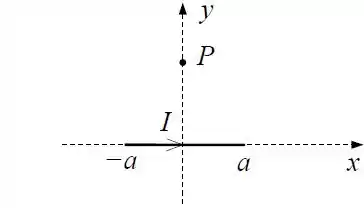
Usando a lei de Biot-Savart, calcule o campo magnético num ponto do eixo .
Calcule o campo magnético no limite em que .
Passo 1
Usando a lei de Biot-Savart, calcule o campo magnético num ponto do eixo .
A Lei de Biot-Savart é dada por:
Como , podemos reescrever a Lei de Biot-Savart como:
Pra começar, vamos analisar graficamente a situação:
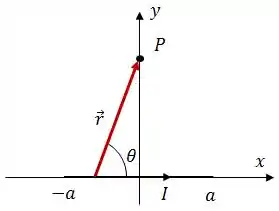
Daqui podemos tirar algumas coisas:
Substituindo isso expressão de , teremos:
Agora vamos organizar esse cara:
Pra finalizar, termos apenas que calcular a integral.
Passo 2
Essa pode ser uma integral bem chata de calcular, mas como é o tipo de integral que aparece bastante nesse tipo de problema, é bem provável que a resposta dela esteja no formulário da prova, então, na dúvida, dê uma olhada lá.
De qualquer forma, integrando a expressão:
Teremos:
Agora é só organizar esse cara:
Finalmente:
Passo 3
Calcule o campo magnético no limite em que .
Beleza, o nosso único trabalho aqui é pegar a expressão de e calcular o limite dela quando , beleza?
Vamos reorganizar esse cara:
Agora, sim. Substituindo por , teremos:
Finalmente:
Resposta