P1 de Probabilidade e Estatística da PUCRIO - 2014.1

b) Defina formalmente uma partição de um espaço amostral. Use o diagrama de Venn para ilustrar.

Você vai fazer uma análise estatística com dados de carros que passam pelas catracas do estacionamento da PUC – Rio. Foram coletados a quantidade, marcas e placas dos veículos que entraram no estacionamento em 1 semana (segunda a sábado; 6 dias).

Considerando somente o último algarismo das placas dos veículos da amostra (0 a 9), responda: (identifique qual é o modelo probabilístico em cada caso).

1. Seja o evento: “o terceiro carro a entrar no estacionamento tem final 1 a 3”. Qual a probabilidade deste sucesso acontecer no terceiro carro a entrar no estacionamento?

Você vai fazer uma análise estatística com dados de carros que passam pelas catracas do estacionamento da PUC – Rio. Foram coletados a quantidade, marcas e placas dos veículos que entraram no estacionamento em 1 semana (segunda a sábado; 6 dias).

Considerando somente o último algarismo das placas dos veículos da amostra (0 a 9), responda: (identifique qual é o modelo probabilístico em cada caso).

Em um determinado período do dia constatou-se que existem somente 20 vagas livres e que nenhum carro iria sair por se tratar de horário de prova. Vinte carros estão na fila para entrar. Qual a probabilidade de menos que 2 carros desta fila serem placa final igual a 3?

c) Seja “” uma v.a. contínua com e é o desvio padrão de . Se , quem é e .

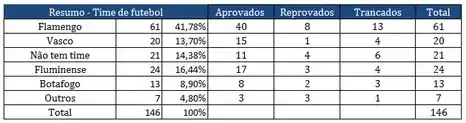
A disciplina PROBEST é obrigatória para a conclusão de vários cursos de graduação do CTC da PUC. No quadro abaixo, apresenta-se o resultado desta disciplina relativo aos alunos matriculados na matéria PROBEST no período passado.

Baseando neste quadro e usando o teorema de BAYES, pede-se:

1. Qual a probabilidade de um aluno ter que repetir (reprovados + trancados) a disciplina PROBEST?
2. Dado que o aluno vai repetir a disciplina, qual a probabilidade do aluno torcer para o time de futebol “Flamengo”.

Seja “” uma variável contínua, onde:

1. O valor de “” para que a função da variável “” seja uma densidade – “”.
2. A função de distribuição da variável “” – “”.
3. Média da variável “” – “.
4. Variância da variável “” – “”.

Você vai fazer uma análise estatística com dados de carros que passam pelas catracas do estacionamento da PUC – Rio. Foram coletados a quantidade, marcas e placas dos veículos que entraram no estacionamento em 1 semana (segunda a sábado; 6 dias).

Considerando somente o último algarismo das placas dos veículos da amostra (0 a 9), responda: (identifique qual é o modelo probabilístico em cada caso).

1. Seja o evento: “o terceiro carro a entrar no estacionamento tem final 1 a 3”. Qual a probabilidade deste sucesso acontecer no terceiro carro a entrar no estacionamento?
2. Em um determinado período do dia constatou-se que existem somente 20 vagas livres e que nenhum carro iria sair por se tratar de horário de prova. Vinte carros estão na fila para entrar. Qual a probabilidade de menos que 2 carros desta fila serem placa final igual a 3?
3. Pelos dados, durante toda a semana (segunda a sábado), passaram pelas catracas 5 carros da marca BMW no estacionamento; ou seja, um evento realmente “raro”. Qual a probabilidade de entrar mais que 2 carros da marca BMW em um dia qualquer da semana?

Os quadros abaixo correspondem aos resultados das notas finais, dos alunos matriculados no período passado na matéria PROBEST 2013-2:

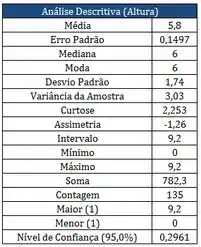
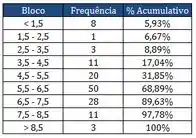
Com relação aos quadrados apresentados, responda as perguntas:

1. O total de alunos que tiraram nota final menor ou igual 4,5 foram 11.

V( ) ou F( )

2. 97,78% dos alunos tem média final menores ou iguais a 8,5.

V( ) ou F( )

3. Pode-se dizer que a Assimetria “-1,26” é uma curva platicurtica.

V( ) ou F( )

4. Quais são as medidas de Localização ou Tendência central?
5. Quais são as medidas de Dispersão?
6. Podemos dizer que a nota final 6,0 é a que mais vezes acontecem.

V( ) ou F( )

7. O coeficiente de variação conforme a estatística descritiva é igual a 3,33.

V( ) ou F( )

8. Construa o diagrama de Pareto desta amostra, montando em blocos conforme o quadro do diagrama de frequência. Esboce os gráficos de frequência e % cumulativo, mostrando os valores correspondentes.