Probabilidade Total e Teorema de Bayes
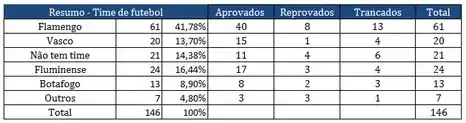
A disciplina PROBEST é obrigatória para a conclusão de vários cursos de graduação do CTC da PUC. No quadro abaixo, apresenta-se o resultado desta disciplina relativo aos alunos matriculados na matéria PROBEST no período passado.
Baseando neste quadro e usando o teorema de BAYES, pede-se:
- Qual a probabilidade de um aluno ter que repetir (reprovados + trancados) a disciplina PROBEST?
- Dado que o aluno vai repetir a disciplina, qual a probabilidade do aluno torcer para o time de futebol “Flamengo”.
Passo 1
(a)
Temos que calcular a probabilidade total de um aluno ter que repetir a disciplina probest, sendo que pra ele repetir pode ser por reprovação ou por ter trancado a matéria.
Vamos chamar de repetir Probest.
Somando ali na tabela a gente vê que 21 alunos reprovaram e 31 alunos trancaram.
Ou seja, 52 alunos vão ter que repetir a matéria.
Passo 2
Como o total são de 146 alunos, podemos dizer que a probabilidade total do aluno repetir a matéria é de:
Passo 3
(b)
Chamando de .
Agora temos que calcular , probabilidade do aluno torcer pro flamengo, sabendo que ele repetiu probest.
Calma! Lê de novo essa parada aí.
Ele quer que você diga a probabilidade do aluno ser de algum time já sabendo que ele repetiu, hmmm, suspeitas de teorema de Bayes.
Passo 4
Usando o teorema de Bayes:
Sendo sagaz, você já notou que a gente conhece todos esses valores aí:
Que a gente acabou de calcular.
Passo 5
Faltou calcular a probabilidade de ele repetir, sabendo que torce pro flamengo, .
Mas tranquilo, a gente soma o número de reprovados e trancados que torcem pro flamengo e divide pelo número total de torcedores do flamengo. Usando a probabilidade condicional.
Passo 6
Agora sim, pra fechar com chave de ouro...
Conclusão dessa questão é que mesmo em um situação fictícia, a torcida do flamengo sempre será a maior.