A barra condutora da figura abaixo tem comprimento e está sendo puxada sobre trilhos horizontais condutores com velocidade constante de módulo , não há atrito entre os trilhos e a barra. Os trilhos estão ligados por uma fita condutora na extremidade direita.
Um campo magnético uniforme de módulo orientado para fora do papel ocupa a região na qual a barra se move.
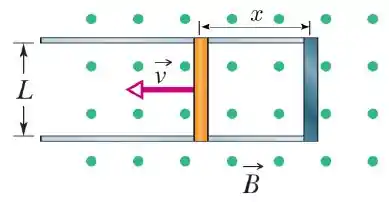
Calcule o módulo do fluxo de através do circuito formado pela barra, a fita e os trilhos no instante em que , onde é a distância entre a barra e a fita, veja a figura.
Calcule o módulo da força eletromotriz induzida na barra.
Suponha que os trilhos e a fita têm resistência desprezível e que a resistência da barra seja .
Encontre o valor da intensidade da corrente induzida na barra e determine se ela está orientada para cima ou para baixo, justifique a sua resposta.
Determine a taxa com a qual energia é dissipada na forma de calor.
Calcule o módulo da força externa que está sendo aplicada na barra.
Passo 1
Calcule o módulo do fluxo de através do circuito formado pela barra, a fita e os trilhos no instante em que , onde é a distância entre a barra e a fita, veja a figura.
O fluxo magnético, por definição, é dado por:
Nesse caso, como o campo magnético é uniforme, o fluxo magnético pode ser escrito como:
Onde é a área da espira, dada por:
Assim:
Onde:
Dessa forma:
Passo 2
Calcule o módulo da força eletromotriz induzida na barra.
De acordo com a Lei de Faraday, a força eletromotriz induzida é dada por:
Sabendo que , o módulo da fem induzida será:
Onde , logo:
Passo 3
Encontre o valor da intensidade da corrente induzida na barra e determine se ela está orientada para cima ou para baixo, justifique a sua resposta.
Vamos começar então calculando a intensidade da corrente induzida.
Uma vez que temos o valor da fem induzida, a corrente induzida será dada por:
Passo 4
Para determinar o sentido da corrente induzida, precisaremos utilizar a Lei de Lenz, que diz que:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Na prática, o que acontece é o seguinte. Conforme a barra se desloca para esquerda, a sua área aumenta, aumentando também o fluxo magnético através do circuito.
Como o fluxo magnético está aumentando, irá surgir um campo magnético induzido que irá se opor ao campo magnético externo.
Dessa forma, se o campo magnético externo está saindo do plano da página, o campo magnético induzido irá entrar no plano da página, como mostra a figura abaixo.
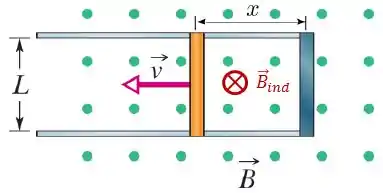
Agora, para determinar o sentido da corrente induzida basta utilizar a regra da mão direita, onde o seu polegar vai apontar na mesma direção e sentido o campo magnético induzido, e os seus outros dedos indicarão o sentido da corrente induzida.
Fazendo isso, vemos que a corrente induzida está no sentido horário, logo, na barra a corrente estará orientada para cima.
Passo 5
Determine a taxa com a qual energia é dissipada na forma de calor.
Se estamos falando de taxa de dissipação de energia, estamos falando em potência dissipada.
Nesse circuito, o único elemento que dissipa energia é a barra, que possui resistência de .
Logo, a potência dissipada no circuito será dada por:
Onde corresponde à corrente induzida que calculamos no Passo 3.
Logo:
Passo 6
Calcule o módulo da força externa que está sendo aplicada na barra.
A fora magnética sobre um condutor retilíneo é dada por:
Onde representa um vetor cujo módulo é igual ao tamanho do condutor, e a direção e sentido são os mesmos da corrente elétrica.
Aqui, como estamos interessados no módulo da força magnética e os vetores e são perpendiculares, teremos:
Resposta
;
;
, orientada para cima na barra;
;
;