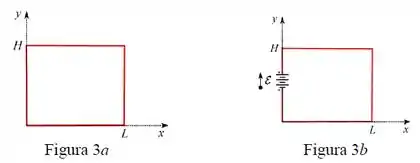
a) Calcule a intensidade e o sentido da força eletromotriz induzida sobre a espira da figura abaixo, dado que na região envolvida existe um campo magnético com módulo , onde e são coordenadas espaciais, é o tempo e é uma constante positiva, apontando para dentro do papel.
b) Uma fonte de força eletromotriz ideal é introduzida na espira, determine a corrente total na espira figura e o seu sentido qualquer instante de tempo , sabendo que a mesma possui uma resistência .
Passo 1
a) A força eletromotriz induzida vai ser dada por
Mas antes vamos encontrar o fluxo magnético pela relação
O campo magnético foi dado pelo problema, e a área da espira é , então:
Passo 2
Com o fluxo magnético em mãos, vamos agora calcular a força eletromotriz beleza?
Passo 3
b) A corrente na espira vai ser a sua força eletromotriz total dividido pela sua resistência, ou seja
A corrente estará no sentido horário.
Resposta
a)
b)