Uma espira é formada por duas partes: um trilho condutor em forma de U invertido, de largura , onde está colocado um resistor e uma haste horizontal condutora (sem massa) que desce em contato com o U invertido e sustenta uma massa (veja figura abaixo).
Esta espira (que está no plano vertical ) é perpendicular a um campo magnético . Suponha que não existam atritos mecânicos no problema.
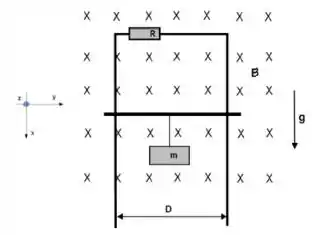
- Situação 1: . Encontre a velocidade final de descida, que é constante, para a massa .
- Situação 2: . Considere, também, que no instante a haste horizontal que sustenta a massa está em uma posição tal que a área formada é igual a . Encontre e de modo que a massa fique sempre estacionária. OBS: Não se preocupe com o instante inicial.
- Para os casos de a) e b), a corrente circula na espira no sentido horário ou anti-horário? Justifique suas afirmações.
- Para o caso b), calcule a potência em função do tempo, para , realizada pelas correntes externas que geram o campo magnético, enquanto a massa fica estacionária.
Passo 1
a) Aqui vemos que, enquanto a massa desce, a área através da qual o campo magnético passa aumenta com o tempo. Isso significa que vai aparecer uma fem induzida que vai se opor à variação temporal do fluxo.
Como o campo magnético neste item é constante, o fluxo magnético será dado por
em que é o comprimento na direção do eixo que está variando com o tempo. Portanto, o módulo da fem induzida será
Como e , teremos que a corrente induzida será
Quando essa corrente passa pela barra condutora, e esta barra é perpendicular ao campo magnético, a força que aparece na barra é
Como a barra tem velocidade constante, , que tem mesma direção e sentido contrário ao da força peso, precisa também ter o mesmo módulo, o que nos dá
Passo 2
b) Neste item, a área permanece fixa no tempo e tem valor , mas o campo magnético varia no tempo. Como o campo magnético está entrando na página, , podemos colocar o vetor área também na mesma direção e sentido: . Por isso, o fluxo magnético será
O módulo da fem induzida é, então,
de onde a gente tira que a corrente induzida tem o seguinte valor
Novamente, quando passa pela barra condutora horizontal, surge também uma força para cima, cujo módulo é dado por
que é igual do peso da barra. O força-peso que atua na passa tem o mesmo valor para todo o tempo , o que significa que a expressão acima à esquerda de tem que ser independente do tempo. Isso só vai acontecer se
Se jogamos de voltamos de volta em , teremos
Portanto, somente para e , a barra fica sempre parada (estacionária) e a área pela qual passa o campo magnético é constante e igual a .
Passo 3
c) Em ambos os itens anteriores temos o campo magnético entrando na página e o fluxo magnético aumentando com o tempo devido ao aumento da área com o tempo (item a) ou devido ao aumento do campo com o tempo (item b com área constante).
Nos dois casos, surge uma corrente induzida que produz um campo magnético induzido cujo fluxo se opõe à variação temporal do fluxo . Por isso, pela lei de Lenz, tem sentido anti-horário nos dois casos e está saindo da página perpendicular a ela.
Passo 4
d) Para o item b), no Passo 2 encontramos que . Para esse valor, temos que a corrente induzida é dada por
O único element do circuito que dissipa energia é o resistor e taxa com que essa energia é dissipada é dada pela potência , ou seja,
Mas no Passo 2, encontramos que a constante é igual a:
Substituindo em , temos
Resposta
- Ambas as correntes no sentido anti-horário;