Uma partícula carregada é solta a partir do repouso em uma região onde existem um campo elétrico e um campo magnético uniformes. Se os dois são paralelos, a trajetória da partícula é:
- Uma circunferência
- Uma parábola
- Uma linha reta
- Uma hélice
- Uma cicloide
Passo 1
Bem, como de costume nosso aqui que tal começarmos fazendo um esqueminha desses campos?
O problema nos disse que temos dois campos uniformes: um elétrico (em azul) e outro magnético (em vermelho)...

Repare que pelo enunciado são campos paralelos (independente do sentido, devem ter a mesma direção).
E de repente a parece aí uma carga que é solta a partir do repouso...
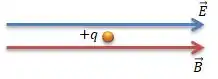
E aí? Qual a trajetória dessa carga? Eis a questão
Passo 2
POW! Devido à presença do campo elétrico, essa carga vai começar a se mover, e no caso, como inserimos uma carga positiva, ela vai se mover para frente...
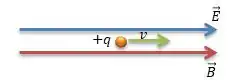
Mas na verdade não importa muito, pois se inseríssemos uma carga negativa, ela ia se mover para trás, mas a trajetória devido ao campo elétrico ia ser a mesma: uma linha reta, saca?
“Tá! Mas e o campo magnético? Não influencia no movimento?”
Passo 3
Então, de acordo com a nossa teoria de magnetismo, o campo magnético só exerce força na carga se a carga tiver uma componente de velocidade perpendicular ao campo magnético!
O que não acontece aqui, já que a velocidade da carga devido a presença do campo elétrico é para sempre na direção paralela a direção do campo magnético, saca? Então o campo magnético não interfere na trajetória da carga!
Outra forma de ver isso é pela expressão da força feita por um campo magnético...
Onde é o ângulo entre a velocidade e o campo magnético. No nosso caso exemplar o ângulo entre a velocidade e o campo magnético é...
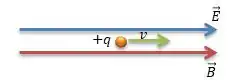
Esse ângulo é ...
Provando que o campo magnético de fato não interfere na trajetória, logo, podemos dizer que a trajetória da partícula é apenas devido a força elétrica feita pelo campo elétrico, ou seja, uma trajetória reta!
Resposta
Letra C