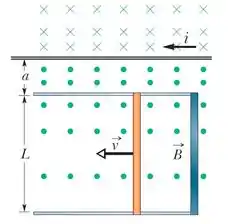
A figura mostra uma barra de comprimento que é forçada a se mover com velocidade escalar constante ao longo de trilhos horizontais. A barra, os trilhos e a fita metálica na extremidade direita dos trilhos formam uma espira condutora. A barra tem uma resistência de 0,400 Ω; a resistência do resto da espira é desprezível. Uma corrente que percorre um fio longo situado a uma distância da espira
produz um campo magnético (não uniforme) que atravessa a espira. Determine (a) a força eletromotriz e (b) a corrente induzida da espira. (c) Qual é a potência dissipada na espira? (d) Qual é o módulo da força que deve ser aplicada à espira para que se mova com velocidade constante? (e) Qual é a taxa com a qual a força realiza trabalho sobre a espira?
Passo 1
Vamos por partes pois o exercício é longo e envolve uma série de conceitos.
Como o exercício está falando de uma espira variando o seu tamanho (área), podemos admitir que se trata de um exercício sobre lei de Faraday.
Primeiro vamos calcular a força eletromotriz induzida:
Vamos chamar a distância entre a barra e a extremidade direita dos trilhos.
Presisamos lembrar da fórmula do campo magnético gerado por um fio em um ponto do espaço:
Sendo a distância entre o ponto e o fio; a corrente no fio e a permeabilidade magnética no vácuo.
Agora vamos considerar uma tira horizontal (paralela ao fio) infinitesimal de comprimento e largura , situada a uma distância r do fio. A área desta tira é: .
Então o fluxo através da tira é:
Como precisamos do fluxo total na área envolvida pela espira formada pela barra e pelos trilhos, temos:
De acordo com a lei de Faraday, a força eletromotriz induzida na espira é:
A única variável que depende do tempo, neste caso, é:
Sabemos lá da física 1 que nada mais é do que a velocidade:
Entao:
Substituindo:
Essa foi a letra (a)! Vamos continuar!
Passo 2
Para encontrarmos a corrente induzida na espira, precisamos lembrar da lei de Ohm:
Ou:
Com as variáveis do problema:
Substituindo:
Agora precisamos descobrir o sentido desta corrente:
Como a barra está se movimentando para a esquerda, a área da espira está aumentando. Portanto, o fluxo do campo magnético também está aumentando.
Pela lei de Faraday, a corrente induzida na espira terá o sentido oposto à essa variação do fluxo do campo magnético. Como o campo magnético está saindo do papel na área da espira, a corrente induzida irá gerar um campo magnético no sentido contrario, ou seja, entrando no papel. Pela regra da mao direita, se o nosso polegar aponta no sentido de entrar na folha, nossos dedos fazem o movimento no sentido horário.
Passo 3
Para resolver a letra (c), precisamos lembrar da fórmula da potência dissipada num resistor (que nesse caso é a resistência da espira):
Substituindo:
Passo 4
Para resolver a letra (d), precisamos considerar que para que a barra se mova com velocidade constante, a resultante das forças que agem sobre a barra deve ser nula. Para isso, a força externa aplicada à barra deve ser igual, em módulo, à força magnética e deve ter o sentido oposto. O módulo da força magnética exercida sobre um segmento infinitesimal da barra de comprimento , situado a uma distância do fio, é
Integrando a força magnética sobre toda a barra:
Substituindo:
Temos que:
Como o campo produzido pelo fio aponta para fora do papel na região onde a barra está se movendo e o sentido da corrente na barra é para cima, a força associada ao campo magnético aponta para a direita (pela regra da mão direita) e, portanto, a força externa aplicada deve apontar para a esquerda.
Passo 5
Finalmente, para resolver a letra (e), precisamos lembrar lá de física 1 que a taxa com que uma força externa realiza trabalho é dada pela fórmula:
Sendo a potência (taxa de energia de trabalho por segundo); a força e a velocidade.
Substituindo:
Como toda a energia fornecida pela força externa é convertida em energia térmica, este valor é igual ao da potência dissipada na espira, calculada na letra (c).
Resposta
(a)
(b) , sentido horário.
(c)
(d)
(e)