3 - Uma barra vertical de comprimento e resistência desliza com velocidade constante sobre dois trilhos paralelos de resistência desprezível, conforme ilustrado na figura abaixo. As extremidades do lado direito de cada trilho estão conectadas por meio de um condutor vertical de resistência desprezível, formando assim um circuito fechado. Todo o conjunto é submetido a um campo magnético uniforme , que aponta para fora da página.

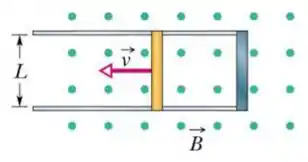
(a) Calcule a força eletromotriz induzida no circuito.

(b) Calcule o valor da corrente induzida no circuito e determine o seu sentido (horário ou anti-horário). Justifique sua resposta.

(c) Qual a potência dissipada na barra vertical de resistência .

(d) Calcule o módulo da força externa exercida na barra para manter sua velocidade constante.

Começando pelo item a), como vamos obter a força eletromotriz induzida no circuito?

Pela lei de Faraday, a força eletromotriz induzida é igual a (menos) a variação do fluxo magnético sobre a variação do tempo, ou seja

Mas o que é ?

Sabemos que a variação do fluxo é igual ao campo magnético multiplicado pela variação da área que flui o campo

Como nossa barra está em movimento, a área interna do circuito aumenta com o tempo.

Em um instante, a área é dada por

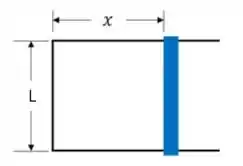
Ou seja, como a área do quadrado é base · altura...

Perceba que é constante e varia com o tempo, então podemos reescrever como

Substituindo em , temos

Essa fração é familiar para você? 👀

A derivada da posição não resulta na velocidade?

Mas como aponta para a esquerda e estamos considerando positivo para a direita, temos

Logo, a força eletromotriz induzida no circuito é dada pelo produto do campo magnético, a distancia e a velocidade .

Bacana, não é? 😁

No item b) vamos calcular a corrente que flui no circuito.

Pela lei de Ohm, a tensão é igual a resistência · a corrente, lembra disso?

Ou seja, como temos apenas uma resistência no circuito

Isolando

Mas não acabamos de encontrar que ?

Então substituindo em vamos obter

Dessa forma, podemos encontrar a corrente que flui pelo circuito! Mas em qual sentido ela flui?? 🤔

Pela lei de Lenz, aplicando a regra da mão direita com a palma voltada para dentro do circuito, como o campo aponta para fora da tela, podemos afirmar que a corrente flui no sentido horário!

Tranquilo até aqui? 👍

No item c) vamos calcular a potência dissipada pela haste de resistência .

A potência dissipada por um resistor em um circuito você lembra como é?

No caso, é a força eletromotriz .

Como no circuito temos apenas nossa haste que está sob ação de uma força eletromotriz e uma corrente , portanto.

Substituindo e , que acabamos de calcular, em , vamos obter.

Resultando em...

Interessante, né? 😎

Por fim, no item d) vamos calcular a força externa que age na barra que faz sua velocidade ser constante.

Como não há atrito da barra com as hastes, se a velocidade é constante, a força resultante que age sobre a barra é .

Mas se , onde é o vetor distancia que segue o sentido da corrente do circuito, temos que aponta para a direita.

Mas como a barra viaja para a esquerda, existe uma força externa atuando na barra apontando para a esquerda e como é constante, essa força externa tem a mesma magnitude da força magnética.

Como aponta para o sentido da corrente, temos que

, no sentido positivo de

Fazendo o produto vetorial de ...

Com isso, vemos que a força magnética resulta em

Como como estamos interessados na magnitude da força externa e como . Temos

Substituindo pelo valor que calculamos a pouco, vamos obter

Simplificando...

E essa é a força externa que mantem a barra em movimento constante.

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍