Considerando que o preço médio de venda (em dólares americanos) do Real nos últimos foi de com desvio padrão de , os limites do intervalo de confiança da média populacional com de confiança são:
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Essa questão é bem rapidinha de resolver, principalmente quando se tem prática no assunto, então lembre-se “a prática leva à perfeição”, então bora praticar!
O enunciado nos deu praticamente tudo, o número de amostras , a média o desvio padrão e o intervalo de confiança de .
O que falta é o , mas podemos calcular com os dados que temos, onde
ou
O que vamos precisar da tabela de índices do grau de liberdade.
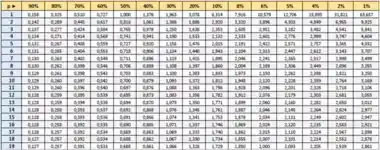
Para descobrir o índice que vamos usar, precisamos calcular o grau de liberdade da nossa questão, onde
Como vamos estimar apenas um valor, vamos usar
Analisando a linha que corresponde ao grau de liberdade e a coluna que corresponde ao que calculamos, vemos que nosso índice
Passo 2
Para concluir a questão, substituímos os valores dados e os valores calculados na fórmula do intervalo de confiança, onde
No lado esquerdo se trata do valor mínimo e no lado direito, o valor máximo do intervalo.
Substituindo , , e , temos
Portanto, nosso intervalo de confiança está entre e , o que corresponde à letra E da questão!

É isso! Entendeu tudo? Responde Aí! 😎👍