Em um experimento foram colhidas amostras de uma população. Todas as amostras tinham o mesmo tamanho e estas amostras também apresentaram as seguintes médias:
![]()
Sabe-se que os valores da média e do desvio padrão populacional são respectivamente e . Se para cada uma destas amostras for construído um intervalo de confiança com de confiança, quantos deles conterão o valor da média populacional?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

A questão nos deu 20 amostras iguais de dados de uma população, onde a média das 20 amostras é 50 , um desvio padrão de 15 e um intervalo de confiança de .
O principal objetivo da questão é responder quantas amostras estão dentro do intervalo de confiança.
Nosso espectro de amostra é
![]()
Resumindo: vamos calcular o intervalo de confiança e contar quantas amostras do nosso espectro estão dentro desse intervalo.
Passo 2
Para calcular o intervalo de confiança, usamos a equação
Utilizando a tabela de índices , vemos que o índice que corresponde ao grau de liberdade, onde
Com , (como vemos na tabela aqui em baixo) e números de amostras .
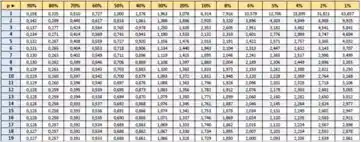
Isso significa que qualquer valor maior que e menor que é englobado na nossa lista.
Por fim, analisando a lista de amostra e comparando cada amostra com o intervalo de confiança, temos que
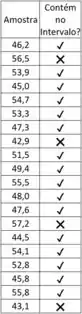
Descobrimos que 16 amostras estão dentro do intervalo de confiança, ou seja, a letra D é a alternativa correta! Muito top né!
É isso! Entendeu tudo? Responde Aí! 😎👍
Resposta
D) 16 Amostras.