Uma empresa fabricante de luvas, antes de lançar um novo modelo de luvas no mercado, deseja realizar um estudo sobre o tamanho das mãos dos indivíduos da população alvo (distância do dedo mindinho ao polegar da mão aberta) a partir de uma amostra aleatória de tamanho . Estudos anteriores mostram que é razoável assumir que essa medida se comporta segundo uma distribuição normal.
a) Qual deve ser o valor de de forma que o intervalo de confiança de 95% para o tamanho médio das mãos dos indivíduos da população, , tenha amplitude menor ou igual a ? ( corresponde ao desvio padrão populacional).
b) Em uma amostra de 400 indivíduos, observou-se média de e variância amostral de . Obtenha um intervalo de confiança de de confiança para o tamanho média das mãos dos indivíduos da população.
c) Um intervalo com uma confiança maior teria amplitude maior ou menor? Justifique.
Passo 1
Eai galerinha, prontos para mais um problema sobre intervalo de confiança?
Temos uma variável que segue uma distribuição normal e queremos brincar com o intervalo de confiança para a média. Nesse primeiro passo vou fazer uma discussão geral que vai nos ajudar a resolver os dois primeiros itens!
A média da distribuição deve seguir uma distribuição normal com média e desvio padrão (desvio padrão da média). Queremos achar o intervalo em torno da média que corresponde a da probabilidade total:
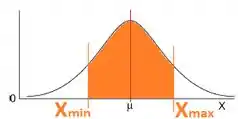
Isso significa que a área da região pintada deve corresponder a . Para resolver esse tipo de problema, nós fazemos uma mudança de variável:
A variável segue uma distribuição normal de média e desvio padrão e é com relação a essa variável que temos as famosas tabelas! Queremos achar os valores de e que correspondem a probabilidade de :
Mas sabemos que pois a distribuição é simétrica, de modo que
Além disso, podemos escrever:
Ou ainda,
Nosso objetivo é achar e, para isso, recorremos à tabela de distribuição:
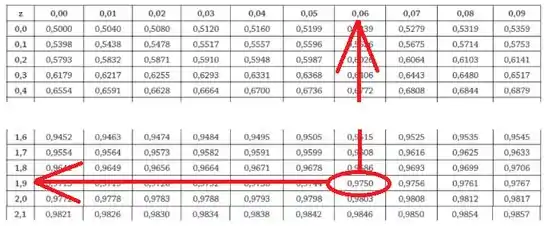
Achamos
Essa resultados será usado nos itens (a) e (b)!
Passo 2
Legal, vamos analisar o item (a)!
Como
Portanto,
Desta forma, o tamanho do intervalo é
Nós queremos que esse intervalo seja menor ou igual a :
Aqui devemos ter um cuidado especial: é o desvio padrão da média e o desvio amostral. Eles se relacionam por
Logo,
Como , temos que
Elevando ao quadrado,
Como não existe um número fracionado de pessoas e se houverem pessoas a condição não é satisfeita, o número mínimo de pessoas que devemos ter na amostra é .
Passo 3
No item (b) temos , e . Primeiro calculamos o desvio padrão da média:
Para achar o intervalo de confiança, precisamos de e :
Como , é só substituir:
Portanto, o intervalo de confiança pedido é
Passo 4
No item (c) ele pergunta o que deve acontecer com a amplitude do intervalo para que o nível de confiança seja maior.
Ora, se a confiança for maior devemos aumentar a área da região em torno da média:
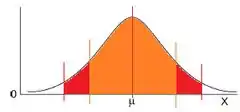
Isso significa que o intervalo deve aumentar, de modo que a amplitude do intervalo de confiança também aumenta!
Resposta
a) pessoas.
b) .
c) Amplitude maior.