Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Intervalo de Confiança para Média com σ Conhecido

Ver Teoria
Exercício 1012345678911121314

Enunciado

Tarefa da aula – 9 – Probabilidade e Estatística (ENG1029) – 2020/2 – Questão 2

Toma-se uma amostra de 25 usuários de um cartão de crédito e observa-se que o gasto médio mensal é de R$ 3.000,00. O desvio padrão é conhecido e igual a R$ 1.200,00.

Pede-se: Encontre os Intervalos de confiança 96% e 98% para o gasto médio com cartão na população de usuários. Deduzir detalhando todos os passos necessários para a construção do Intervalo de confiança – IC.

Passo 1

O problema forneceu para gente uma amostra com 25 usuários de um cartão de crédito, ou seja, 25 variáveis aleatórias que seguem uma distribuição normal:

n = 25

E o enunciado nos deu também, o gasto médio mensal desses usuários, que é...

X = 3000

O desvio padrão também é conhecido, é igual à...

σ = 1200

Ora bolas! Temos aí um intervalo de confiança para média, com σ conhecido!

Passo 2

Sendo assim, vamos usar a fórmula abaixo...

I C = X - ± z 1 - α 2 ⋅ σ n

Bom! O primeiro intervalo de confiança dado é o de 96 % . Logo;

1 - α = 0,96

α = 0,04

E então, temos que...

z 1 - α 2 = z 1 - 0,04 2 = z 0,98

Substituindo na fórmula...

I C = X - ± z 0,98 ⋅ σ n

Ao dar uma olhada na tabela abaixo...

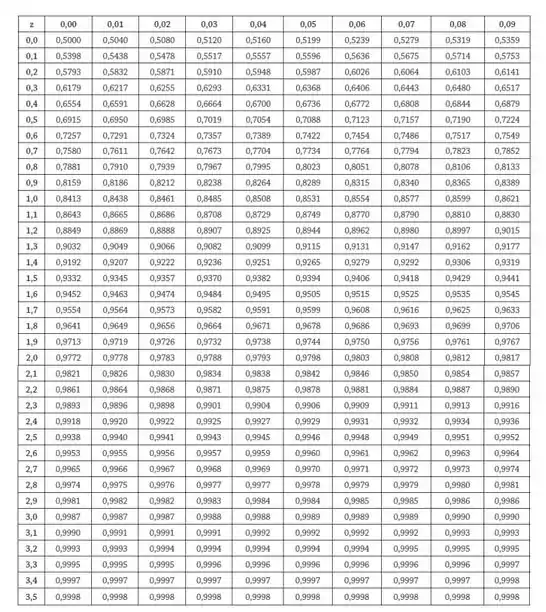
Podemos ver que...

z 0,98 ≅ 2,06

Desse modo, substituindo os valores numéricos, obtemos que...

I C = 3000 ± 2,06 ⋅ 1200 25

I C = 3000 ± 494

I C = [ 2506 ; 3494 ]

Passo 3

Pro segundo intervalo de confiança, de 98 % , basta repetir o mesmo procedimento...

Primeiro descobrimos α :

1 - α = 0,98

α = 0,02

E então;

z 1 - α 2 = z 1 - 0,02 2 = z 0,99

Substituindo na fórmula...

I C = X - ± z 0,99 ⋅ σ n

Ao olhada a tabela, descobrimos que...

z 0,99 = 2,33

Sendo assim, obtemos o seguinte resultado...

I C = 3000 ± 2,33 ⋅ 1200 25

I C = 3000 ± 559

I C = [ 2441 ; 3559 ]

Pronto! Finalizamos aqui!

Resposta

P a r a   96 % :   I C = [ 2506 ; 3494 ]

P a r a   98 % :   I C = [ 2441 ; 3559 ]

Exercícios de Livros Relacionados

Considere a distribuição de uma população normal com o valor de σ conhecido.a. Qual é o nível de confiança do intervalo x ‾ ± 2,81 σ / n ?b. Qual é o nível de confiança do intervalo x ‾ ± 1,44 σ / n ?
Considere os próximos 1000 ICs de 95 % de μ que um consultor estatístico obterá para vários clientes. Suponha que os conjuntos de dados em que os intervalos se baseiam sejam selecionados independentem
Seja α 10 , α 20 , c o m ⁡ α 1 + α 2 = α .Então , ã P - z α 1X - - μ σ / nz α 2 = 1 - α a. Use essa equação para deduzir uma expressão mais geral para um IC de 100 ( 1 - α ) % de μ do qual o intervalo
Com base em testes extensivos, o ponto de escoamento de um tipo específico de barra de aço reforçado é conhecido por ser normalmente distribuído c o m ⁡ σ = 100 . A composição da barra foi levemente m
O tempo entre a carga e o final do processo (min) de um aço carbono em um tipo de fornalha aberta foi determinado para cada aquecimento em uma amostra de tamanho 46 , resultando um tempo médio amostra