Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Intervalo de Confiança para Média com σ Conhecido

Ver Teoria
Exercício 1312345678910111214

Enunciado

USP. Estatística. Prova P1. 2018.2. Teste 7.

Um instituto de pesquisa foi contratado por um partido para fazer um levantamento sobre a popularidade do seu candidato a um cargo eletivo entre os eleitores. O instituto então entrevistou 100 eleitores selecionados segundo uma amostra aleatória simples e questionou os mesmos se eles apoiariam o candidato. Apenas 10 % dos entrevistados disseram que sim. Com 98 % de confiança, quais os limites do intervalo de confiança para a real intenção de voto neste candidato?

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

O enunciado nos disse que foi realizada uma votação e obtiveram 100 amostras dessas amostras 10% votaram positivo e 90% votaram negativo, o objetivo principal da questão é calcular os limites de votos positivos a partir do nível de confiança de 98%.

Foram dados poucos dados, o que pode nos deixar um pouco confusos de início. Mas não se preocupe, temos dados o suficiente para calcular nosso intervalo de confiança.

Não temos o desvio padrão, portanto não podemos usar a equação usual do intervalo de confiança. Neste caso, como lidamos com porcentagem, calculamos o erro de outra forma.

Se no começo parecia que estava confuso e agora parece que está no começo, vamos para os cálculos que não vai ter erro!

Passo 2

Como dito anteriormente não temos o desvio padrão e estamos trabalhando com porcentagens dessa forma como vamos calcular o erro?

Nestes casos, o erro é calculado a partir da fórmula

E r r o = p 1 - p n

Onde p é a porcentagem obtida p = 0.1 e n é a quantidade de amostras n = 100

Assim podemos unir a fórmula convencional do cálculo de intervalo de confiança com a equação descrita anteriormente, resultando em

I C = p ± Z · E r r o

I C = p ± Z · p 1 - p n

p já foi definido e Z é um valor tabelado que corresponde a um índice relacionado ao nível de confiança que desejamos obter. No caso...

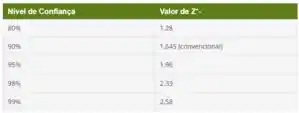
Como desejamos obter um nível de confiança de 98% nosso índice Z é igual a 2.33 .

Passo 3

Temos o valor de p , o valor de Z e a formula do erro.

Com isso nosso intervalo de confiança será

I C = p - Z · p 1 - p n ;   p + Z · p 1 - p n

Substituindo p = 0.1 , Z = 2.33 e n = 100 , temos

I C = 0.1 - 2.33 · 0.1 1 - 0.1 100 ;   0.1 + 2.33 · 0.1 1 - 0.1 100

I C = 0.1 - 2.33 · 0.03 ;   0.1 + 2.33 · 0.03

I C = 0.03 ; 0.17 ou I C = 3 % ; 17 %

A partir dos cálculos, de acordo com o nível de confiança de 98% nosso intervalo de confiança varia entre 3 % e 17 % . Com esse resultado vemos que a alternativa correta é a letra A)!

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

A) I C = 3 % ; 17 %

Exercícios de Livros Relacionados

Considere a distribuição de uma população normal com o valor de σ conhecido.a. Qual é o nível de confiança do intervalo x ‾ ± 2,81 σ / n ?b. Qual é o nível de confiança do intervalo x ‾ ± 1,44 σ / n ?
Considere os próximos 1000 ICs de 95 % de μ que um consultor estatístico obterá para vários clientes. Suponha que os conjuntos de dados em que os intervalos se baseiam sejam selecionados independentem
Seja α 10 , α 20 , c o m ⁡ α 1 + α 2 = α .Então , ã P - z α 1X - - μ σ / nz α 2 = 1 - α a. Use essa equação para deduzir uma expressão mais geral para um IC de 100 ( 1 - α ) % de μ do qual o intervalo
Com base em testes extensivos, o ponto de escoamento de um tipo específico de barra de aço reforçado é conhecido por ser normalmente distribuído c o m ⁡ σ = 100 . A composição da barra foi levemente m
O tempo entre a carga e o final do processo (min) de um aço carbono em um tipo de fornalha aberta foi determinado para cada aquecimento em uma amostra de tamanho 46 , resultando um tempo médio amostra