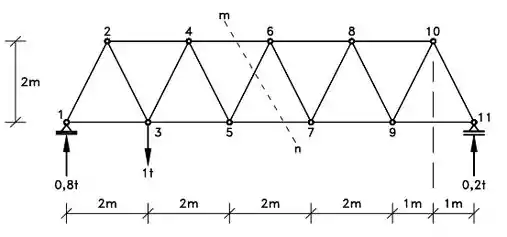
Considere a treliça abaixo e determine as forças nas barras 4-6, 5-6 e 5-7. Para isso obrigatoriamente use o corte da seção definida por M-N. (Considere 0,8 t e 0,2 t como as forças realizadas pelos apoios)
Passo 1
Faaala, nessa questão o professor, já especificou que precisaremos usar o corte M-N, para resolver a questão correto?
Significa então, que precisaremos utilizar o método das seções para poder determinar cada reação nas barras!
Nosso primeiro passo é escolher qual lado da treliça utilizar. Alguma ideia?
É isso mesmo que você está pensando... vamos utilizar o lado direito da treliça, pois o lado direito apresenta menos forças de reação do que o lado esquerdo, pelo falo de ter um apoio de primeiro gênero!
A princípio sempre é bom escolhermos o lado com menor número de reações.
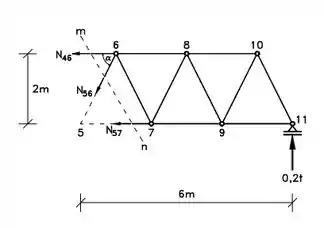
Visto isso, teremos;
Passo 2
Agora com o lado da treliça escolhido, iremos aplicar as fórmulas de equilíbrio.
Importante (Vale lembrar que se a treliça toda está em equilíbrio, uma seção qualquer dela também está em equilíbrio)!Somatório dos momentos em relação ao Nó 5;
Somatório dos momentos em relação ao ponto 6;
Somatório das forças na vertical;
Agora temos um problema, como encontrar α?
Uma observação pontual pode resolver esse problema! Você reparou que podemos usar as propriedades de trigonometria e teremos que;
Retornando a conta da reação;
Resposta
As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.