Determine os esforços normais nas barras CD, ID e IJ e comprove pelos dois lados da treliça o resultado encontrado. Justifique o motivo do resultado encontrado.
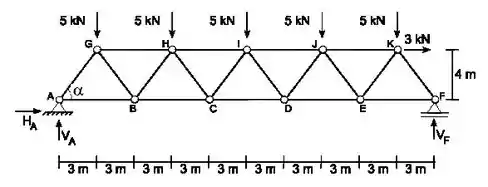
Passo 1
Fala pessoal, vamos ver mais essa questão sobre método das seções!
Vale ressaltar que dessa vez o enunciado quer que a gente comprove o nosso resultado pelos dois lados da treliça, ou seja vamo precisar realizar os cálculos tanto na seção esquerda quanto na seção direita do corte! Boraaaa?Primeiro precisamos verificar quais são os valores das reações dos apoios! Partiu???
Somatório dos momentos em relação ao ponto A:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 2
Vamos escolher um corte que passe pelas três barras que desejamos determinar as reações.
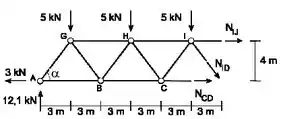
Agora que temos o corte definido vamos precisar analisar os dois lados, para determinar o que pede o enunciado.
Vamos começar pelo lado esquerdo da treliça;
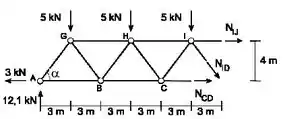
Podemos observar que temos um ângulo α°, e precisamos determinar ele certo?
Usando as regras da trigonometria do ensino médio vamos obter;
Assim;
Agora podemos fazer o somatório das forças verticais igual a zero;
Somatório dos momentos em relação ao ponto I igual a zero;
Somatório dos momentos em relação ao ponto D igual a zero;
Passo 3
Agora vamos refazer todos os cálculos só que tendo como referencial a seção direita da treliça;
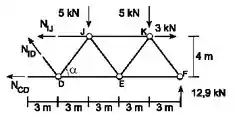
Agora podemos fazer o somatório das forças verticais igual a zero;
O valor de Nid, bateu com a resposta anterior encontrada.
Somatório dos momentos em relação ao ponto I igual a zero;
O valor de Ncd, bateu com a resposta anterior encontrada.
Estamos quase láaa! Desiste não...
Somatório dos momentos em relação ao ponto D igual a zero;
O valor de Fcd, bateu com a resposta anterior encontrada.
Resposta
As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.
A resposta pode ser justifica, pelo fato de que toda vez que um corpo está em equilíbrio, é correto considerar que qualquer parte do mesmo também estará em equilíbrio, ou seja , independente de qual parte da treliça estudarmos, ambas vão estar em equilíbrio e manter suas respectivas reações de compressão ou tração. Por isso independe o caminho ou o lado que iremos escolher para achar os resultados.