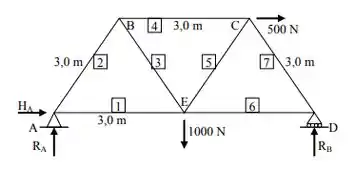
Resolva a treliça abaixo pelo método das seções e determine as reações nas barras 1, 3 e 4.
Passo 1
E aíii, beleza? Vamos ver mais essa questão juntos?
Bom como pudemos observar, o enunciado foi bem claro, deixou bem especificado que ele deseja utilizar o método das seções, para achar as forças de reação nas barras 1,3 e 4.
Para utilizar o método, primeiro precisamos verificar quais são os valores das reações dos apoios! Bora lá?

No nó A tempos um apoio de segundo gênero, dessa forma teremos uma força na horizontal e uma na vertical (Ha e Ra) e no nó D temos um apoio de primeiro gênero, com uma única reação na vertical (Rd).Dessa forma, podemos agora determinar o valor das reações.
Pera, pera, antes precisamos descobrir os ângulos entre as barras e a altura h , presente na treliça, não podemos esquecer disso!
Vamos observar a seção triangular composta pelas barras 1, 2 e 3.Como podemos perceber, ela tem uma seção triangular de lado igual a 3 metros, o que significa que teremos um triângulo equilátero, por consequência o ângulo α° = 60°, e a altura vai originar da fórmula da altura de um triângulo equilátero lá do ensino médio, que é:
Agoraaa sim, podemos voltar para o equilíbrio da treliça, então teremos;
Somatório dos momentos em relação ao ponto A:
Somatório das forças verticais iguais a zero
Somatório das forças horizontais iguais a zero:
Passo 2
Agora é a hora de separar as seções!
Eu pensei em dois possívei cortes, vou colocar eles aqui e aí você me ajuda a decidir qual é o melhor pode ser?
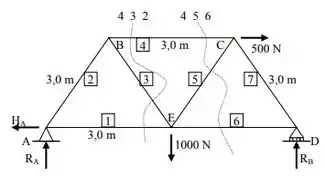
Não sei se faço o corte 4,3,2 ou o 4,5,6! Tá difícil a escolha....
Sabe porquê essa escolha se torna difícil?
Pois a princípio são cortes muito similiares, devido a treliça ter seções triangulares semelhantes, mas como nosso objetivo é descobrir as reações nas barras 1, 3 e 4, seria melhor se fizermos o corte 4,3,2 pois ele passa por mais elementos que desejamos encontrar.
Assim se fizermos um DCL desse corte teremos;
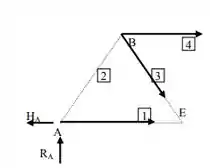
Agora vamos calcular o equilíbrio dos momenos em relação ao ponto B, vamos chamar de F1 a força realizada na barra 1;
Agora vamos calcular o equilíbrio dos momenos em relação ao ponto E, vamos chamar de F4 a força realizada na barra 4;
Agora vamos calcular o equilíbrio dos momenos em relação ao ponto A, vamos chamar de F3 a força realizada na barra 3;
Resposta
As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.