Determinar as forças normais nas barras da treliça dada
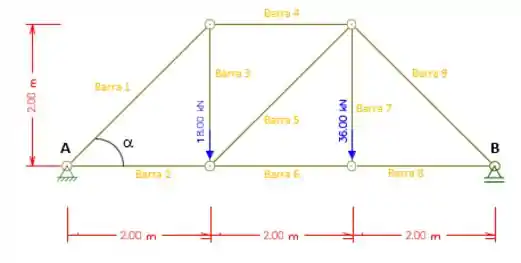
Passo 1
Cara, o enunciado diz para gente que precisamos determinar todas as reações de cada barra da treliça.
Se você percebeu , o único dado que não recebeu nenhum valor numérico foi o ângulo α.
Mas, como eu acho o ângulo α, já que ele não foi dado? Vem comigo que eu te mostro...
Se a gente observar bem, temos um triângulo retângulo isósceles, visto que a Barra 3 e a Barra 2 são perpendiculares entre si e ambas medem 2 m. Dessa forma conseguimos provar que o ângulo α = 45°. Ahh, mas eu não consegui ver o motivo de ser 45°, vamos lá fazer a conta então.
Passo 2
Agora podemos calcular as reações de apoio, porém para isso precisamo representar as forças na treliça, dessa forma iremos pintar de rosa as reações de apoio;
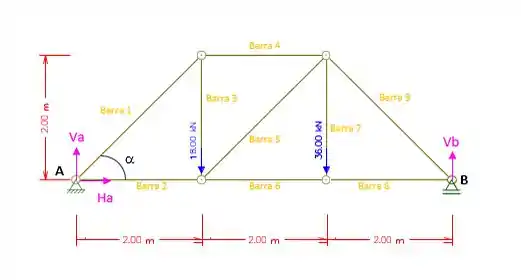
Somatório dos momentos em relação ao ponto A:
Somatório das forças horizontais iguais a zero:
Passo 3
Agora vamos fazer um corte AA representado pela figura abaixo, para determinar as formas nas barras 1 e 2.
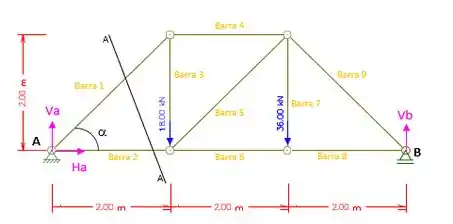
Somatório das forças verticais iguais a zero:
(Barra Comprimida)
Somatório das forças horizontais iguais a zero:
(Barra Tracionada)
Passo 4
Agora vamos fazer um corte BB representado pela figura abaixo, para determinar as formas nas barras 3 e 4.
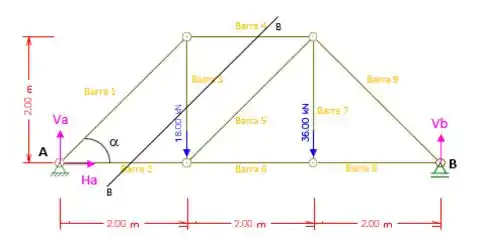
Somatório das forças verticais iguais a zero:
(Barra Tracionada)
Somatório dos Momentos em D igual a zero:
(Barra Comprimida)
Passo 5
Agora vamos fazer um corte CC representado pela figura abaixo, para determinar as formas nas barras 5 e 6.
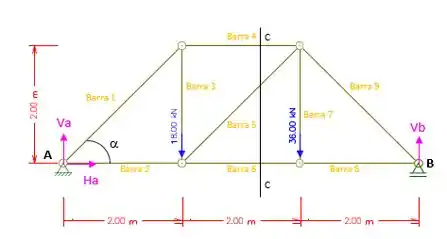
Somatório das forças verticais iguais a zero:
(Barra Comprimida)
Somatório dos Momentos em E igual a zero:
30 KN (Barra Tracionada)
Passo 6
Agora vamos fazer um corte DD representado pela figura abaixo, para determinar as formas nas barras 7 e 8. (Super Dica: As vezes fazer seções curvas pode facilitar muito as contas para isolar uma seção especial)
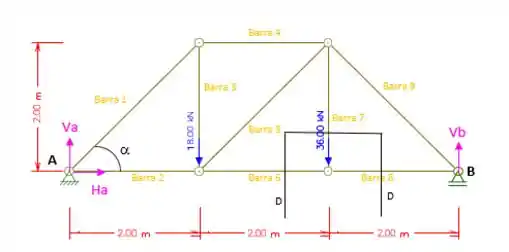
Somatório das forças verticais iguais a zero:
(Barra Tracionada)
Somatório das forças horizontais iguais a zero:
30 KN (Barra Tracionada)
Resposta
Agora vamos fazer um corte EE representado pela figura abaixo, para determinar a forma na barra 9.
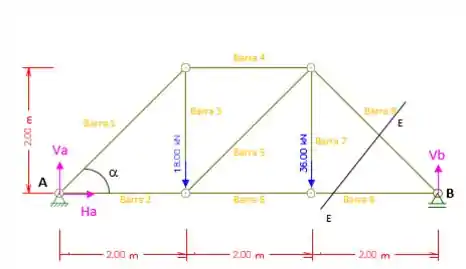
Somatório das forças verticais iguais a zero:
(Barra Comprimida)
Resposta
(Barra Comprimida)
(Barra Tracionada) (Barra Tracionada) (Barra Comprimida)
(Barra Comprimida)
30 KN (Barra Tracionada)
(Barra Tracionada) 30 KN (Barra Tracionada)
(Barra Comprimida)