Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método da seção de Richter Barras Secundarias

Ver Teoria
Exercício 81234567

Enunciado

Determinar as forças normais nas barras da treliça dada.

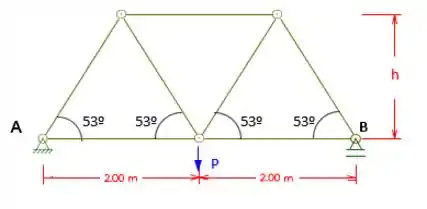
Passo 1

Vamos entender o enunciado... Bora lá?

De acordo com enunciado, precisamos encontrar todas as forças em todas as barras.

Porém antes, precisamos comentar duas coisas... a primeira é, você deve ter reparado que temos um h e um P que não estão identificados na questão correto?

Não se preocupe com isso, o h você vai ver comigo que vamos poder encontrar, porém o P é um valor incógnita, ou seja a resposta ficará em função de P. Você verá no final...

Agora vamos marcar as forças de reação na treliça em laranja, marca aí...

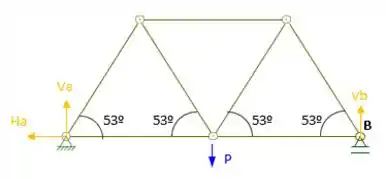
Não se esqueça, quando temos um apoio de primeiro gênero como o do ponto B, temos apenas esforço na vertical e quando temos um apoio de segundo gênero como o do ponto B, teremos esforço na horizontal e na vertical!Mais uma dica importante, você pode arbitrar a o sentido das forças como achar melhor ou até mais bonitinho, rs!

Pois caso você escolha uma direção e ela esteja errada, você vai encontrar no final o resultado com uma resposta negativa, e na mecânica resultados negativos caracterizam, que a direção é ao contrário do que arbitrou inicialmente!

Passo 2

Boa, agora que já marcamos as reações dos apoios, podemos descobrir outras informações sobre a treliça... Tô muito curioso para descobrir o valor de h, você não? Então vamor lá...

A altura h ela pode ser encontrada de diversas formas, porém a mais fácil e visual é através da aproximação a tangente, assim:

h = T g 53 ° =   1,33 m  

Cara, existe mais uma coisa que pode facilitar nossa vida, se você reparar devido à simetria da estrutura e do carregamento, podemos afirmar que:

- V a = - V b = - P 2

Passo 3

Agora, para determinar a carga axial nas barras 1 e 2, aplica-se o corte AA e BB como na figura abaixo.

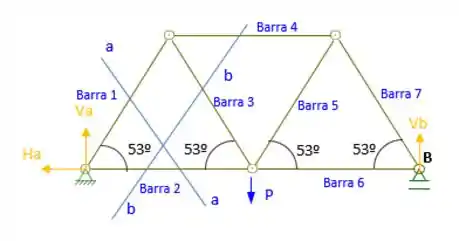
Para a parte esquerda do corte AA podemos obter:

Somatório das forças verticais igual a zero:

∑ F y = 0 F 1 ⋅ s e n 53 ° + P 2 = 0 F 1 = - P 2 ⋅ s e n 53 ° F 1 = - 0,625 P (Barra Comprimida)

Somatório das forças horizontais igual a zero:

∑ F x = 0 F 2 + F 1 ⋅ cos ⁡ 53 ° = 0   F 2 - 0,625 ⋅ P ⋅ cos ⁡ 53 ° = 0 F 2 = 0,375 ⋅ P (Barra Tracionada)

Para o corte BB podemos obter as forças nas barras 3 e 4:

Somatório dos momentos em relação ao ponto E:

∑ M = 0 1,33 ⋅ F 4 + 2 ⋅ P 2 = 0 F 4 =   - P 1,33 F 4 =   - 0,75 P (Barra Comprimida)

Somatório das forças verticais igual a zero:

∑ F y = 0 F 3 ⋅ s e n 53 ° - P 2 =   0   F 3 ⋅ s e n 53 ° = P 2 F 3 = P 2 ⋅ s e n 53 ° F 3 = 0,625 P (Barra Tracionada)

Super Dica: Como a treliça é simétrica, podemos concluir que:

F 7 = F 1 =   - 0,625 ⋅ P F 6 = F 2 = 0,375 ⋅ P F 5 = F 3 = 0,625 ⋅ P

Resposta

F 1 = - 0,625 ⋅ P (Barra Comprimida) F 2 = 0,375 ⋅ P (Barra Tracionada) F 3 = 0,625 ⋅ P (Barra Tracionada) F 4 =   - 0,75 ⋅ P (Barra Comprimida) F 5 =   0,625 ⋅ P (Barra Tracionada) F 6 = 0,375 ⋅ P (Barra Tracionada) F 7 =   - 0,625 ⋅ P (Barra Comprimida)

Exercícios de Livros Relacionados

A treliça mostrada é formada por triângulos retângulos de 45 ° . Os elementos cruzados nos dois painéis centrais são barras de amarração esbeltas incapazes de suportar compressão. Mantenha as duas bar
Calcule as forças nos elementos B C , B EeE F . Determine cada força a partir de uma equação de equilíbrio que a contenha como a única incógnita.
Determine a força no elemento C K da treliça carregada.
Determine a força no elemento J M da treliça carregada.
Os quadros articulados A C E e D F B estão ligados por duas barras articuladas, A B e C D , que se cruzam sem estarem interligadas. Calcule a força em A B .