Determine atráves do método das seções, as forças normais nas barras 3, 5 e 6.
Passo 1
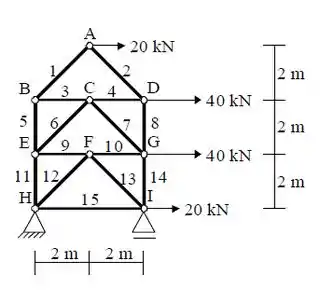
Como o nosso enunciado já diz, precisaremos determinas as forças nas barras 3, 5 e 6! Certo?Para isso vamos precisar pensar quais seções vamos precisar separar para podermos calcular as forças nas barrras acima descritas?Para isso temos que pensar na forma que a treliça ocupa! Ela é completamente simétrica entã seria vantajoso cortar a treliça em maior partes iguais para justificar simetrias! Pescou?
Assim, nossa primeira seção vai ser limitada por um corte que passa pelas barras 5,3,4 e 8. Como na figura abaixo!
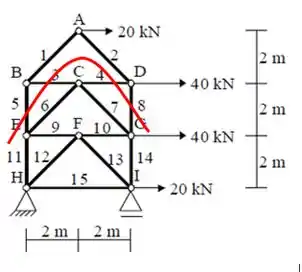
Assim, iremos analisar então a parte superior ao corte e poderemos calcular as reações;
Somatório dos momentos em relação ao ponto D:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 2
Agora é a hora de separar novas seções que ainda possam nos ajudar!Como só achamos o falor de F5, ainda precisamos encontrar F3 e F6. Então nosso próximo passo vai ser cortar as barras em 5, 6, 7 e 8.
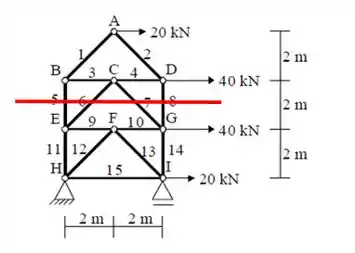
Assim, iremos analisar então a parte superior ao corte e poderemos calcular as reações;Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Por último temos que encontrar ainda a força em 3, para isso vamos cortar a treliça passando pelas barras 2, 3 e 5.
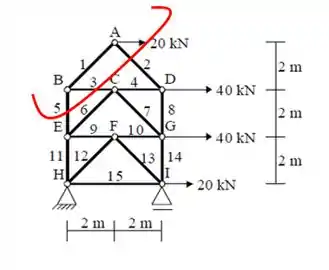
Assim, iremos analisar o último corte!
Somatório dos momentos para um lado superiror da seção!