Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método da seção de Richter Barras Secundarias

Ver Teoria
Exercício 21345678

Enunciado

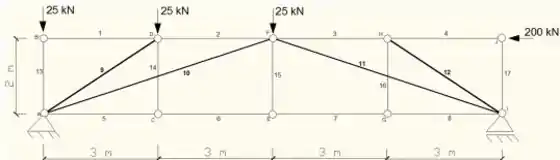
Empregando necessariamente o processo das seções, determinar as forças normais nas barras 9, 10, 11 e 12 da treliça da figura, indicando claramente se essas forças são de tração ou de compressão. No final, escreva essas normais obtidas no espaço indicado.

Passo 1

Fala pessoal, vamos ver mais essa questão sobre método das seções!Primeiro precisamos verificar quais são os valores das reações dos apoios! Bora lá?No nó A tempos um apoio de segundo gênero, dessa forma teremos uma força na horizontal e uma na vertical (Ax e Ay) e no nó I temos um apoio de um gênero, com uma única reação na vertical (Iy).Dessa forma, podemos agora determinar o valor das reações.

Somatório dos momentos em relação ao ponto A:

∑ M a = 0 - I y ⋅ 12 m - 200 ⋅ 2 m + 25 ⋅ 6 m + 25 ⋅ 3 m =   0 - I y ⋅ 12 =   175 I y =   - 14,58   K N Somatório das forças verticais iguais a zero:  

∑ F y = 0 A y + I y - 25 - 25 - 25 = 0 A y - 14,58 = 75 A y = 75 + 14,58 A y = 89,58   K N

Somatório das forças horizontais iguais a zero:

∑ F x = 0 A x - 200 = 0 A x = 200   K N

Passo 2

Agora é a hora de separar novas seções que ainda possam nos ajudar!Como ainda precisamos encontrar N10, então nosso próximo passo vai ser realizar um corte passando nas barras em 2,10 e 6. Para facilitar nossas contas.

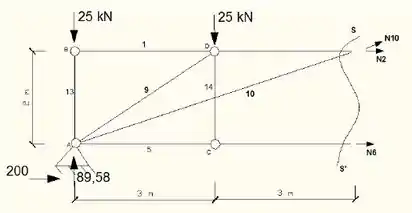
Assim, iremos analisar então a parte superior ao corte e poderemos calcular as reações; Somatório das forças verticais iguais a zero: (Super Dica, para encontrar o ângulo(Ѳ) que é o ângulo de encontro com a barra 10 e a barra 5 precisamos realizar trigonometria para triângulos retângulos  

∑ F y = 0 N 10 ⋅ s e n Ѳ ° + 89,58 - 25 - 25 = 0 N 10 ⋅ s e n Ѳ = - 39,58 N 10 =   - 125,17   K N

(Super Dica, para encontrar o ângulo(Ѳ), que é o ângulo de encontro entre as barras 10 e 5 precisamos realizar trigonometria para triângulos retângulo)

T g Ѳ ° = 2 6 T g Ѳ ° = 1 3 Ѳ = 18,43 °

Logo,

S e n 18,43 ° = 0,3162 C o s 18,43 ° =   0,94 87

Passo 3

Agora vamos aproximando o corte do nó B, para facilitar na identificação das forças, ajudando principalmente a encontrar o valor de força exercida na barra 9. Bora lá?

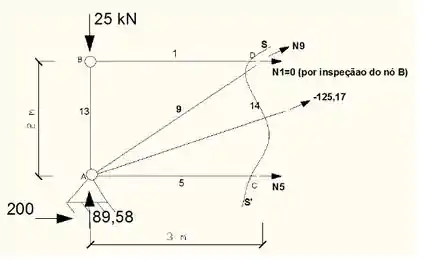
Somatório dos momentos em relação ao ponto C;

∑ M c = 0 N 9 ⋅ cos ⁡ α ° ⋅ 2 m + 89,58 ⋅ 3 m - 125,17 ⋅ cos ⁡ Ѳ ° ⋅ 1 m - 25 ⋅ 3 m =   0 N 9 ⋅ 0,832 ⋅ 2 =   - 268,74 + 118,7 + 75 N 9 ⋅ 1,664 =   - 75,4 N 9 =   - 45,3   K N

(Super Dica, para encontrar o ângulo(Ѳ), que é o ângulo de encontro entre as barras 10 e 5 precisamos realizar trigonometria para triângulos retângulo)

T g α ° = 2 3 α = 33,69 °

Logo,

S e n 33,69 ° = 0,554 C o s 33,69 ° =   0,832

Passo 4

Agora vamos olhar para o lado direito da treliça, para encontrar o valor de força exercida na barra 11. Vamos? Não desanima não!

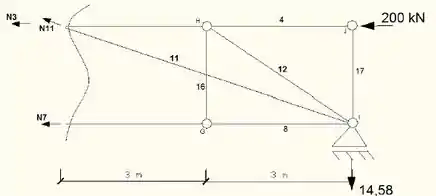
Somatório das forças verticais igual a zero;

∑ F y = 0 N 11 ⋅ s e n Ѳ ° - 14,58 = 0 N 11 = 14,58 0,3162 N 11 = 46,11   K N

Passo 5

Agora vamos aproximar mais o corte para direita, para encontrar o valor de força exercida na barra 12. Partiu?

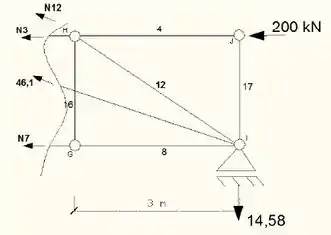
Somatório das forças verticais igual a zero;

∑ F y = 0 N 11 ⋅ s e n Ѳ ° + N 12 ⋅ s e n α ° -   14,58 = 0 N 12 ⋅ 0,554 = 14,58 - 46,11 ⋅ 0,3162 N 12 ⋅ 0,3162 = 14,58 - 14,58 N 12 ⋅ 0,3162 = 0 N 12 = 0

Resposta

N 9 =   - 45,3   K N N 10 =   - 125,17   K N N 11 = 46,11   K N N 12 = 0   K N

As forças com sinal positivo são forças de tração, já as com sinal negativo são forças de compressão.

Exercícios de Livros Relacionados

A treliça mostrada é formada por triângulos retângulos de 45 ° . Os elementos cruzados nos dois painéis centrais são barras de amarração esbeltas incapazes de suportar compressão. Mantenha as duas bar
Calcule as forças nos elementos B C , B EeE F . Determine cada força a partir de uma equação de equilíbrio que a contenha como a única incógnita.
Determine a força no elemento C K da treliça carregada.
Determine a força no elemento J M da treliça carregada.
Os quadros articulados A C E e D F B estão ligados por duas barras articuladas, A B e C D , que se cruzam sem estarem interligadas. Calcule a força em A B .