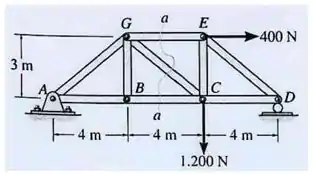
Determine a força nos elementos GE,GC e BC da treliça mostrada abaixo. Indique se os elementos estão sob tração ou compressão.
Passo 1
Bom, precisamos começar entendendo o enunciado,
De acordo com o enunciado, para esse exercício precisaremos calcular as reações nos elementos GE, GC e BC, a fim de entender quais elementos estão sobre tração e quais sobre compressão, mas dessa vez usando o método das seções. Bora lá?
Agora, precisamos entender quais são as reações nos apoios nessa treliça;
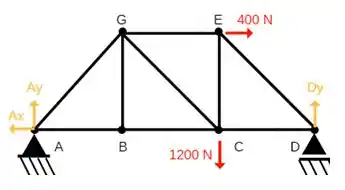
Temos dois apoios, um apoio de segundo gênero no ponto A e um apoio de primeiro gênero no ponto D.
No apoio do ponto A, existem uma reação Ax e uma reação Ay, visto que temos um apoio de segundo gênero.
Já no apoio do ponto D, existe apenas uma reação Dy, visto que temos um apoio de primeiro gênero.
O DCL do corpo ficará assim;
Passo 2
Agora, vamos escolher a melhor seção para dividir treliça!
Nesse exemplo cara, o enunciado facilitou um pouco a nossa vida, pois ele já deixou indicado que a melhor seção para cortarmos é a seção a-a.
Assim com o corte a treliça ficará dessa forma:
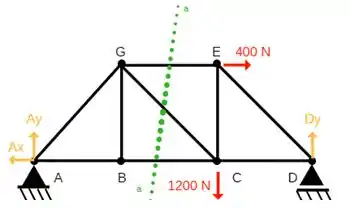
Mas porquê a melhor opção seria cortar a treliça nessa posição?
Essa posição foi escolhida, pois o corte nessa posição passa pelas três barras que precisamos determinar as reações. (Essa é uma dica muito importante, sempre corte as seções nos locais que seja possível pegar o maior número possível de barras que você deseja encontrar as reações)
Passo 3
Não me abandonou? Então continua aqui comigo...
Agora vamos determinar as reações externas em A e D, ou seja as reações dos apoios. Para isso precisamos aplicar as equações de equilíbrio, são elas:
Somatório das forças horizontais igual a zero:
Somatório dos momentos igual a zero:
Somatório das forças verticais igual a zero:
Passo 4
Vamos lá, já determinamos os valores de todas as reações externas, agora precisamos encontrar as reações nas barras desejadas! Para isso vamos isolar a seção da esquerda da treliça. (Super Dica: Tanto faz qual seção isolar, porém escolha sempre a que lhe parece ter contas mais fáceis, ou seja menos reações totais).
Vamos começar analisando a seção esquerda;
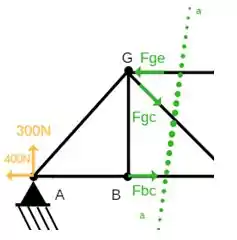
Somatório dos momentos em relação ao ponto G igual a zero: (Super Dica: escolha o ponto que tiver mais forças sendo aplicadas, para ser o referencial, para que elas sumam na conta)
(TRAÇÃO)
Da mesma forma, o somatório dos momentos em relação ao ponto C fornece uma solução direta para Fge;
(COMPRESSÃO)
Visto que Fbc e Fge não apresentam componentes verticais, o somatório das forças na direção vertical fornece diretamente Fgc, em outras palavras:
Somatório das forças verticais igual a zero:
(TRAÇÃO)
Resposta
(TRAÇÃO)
(COMPRESSÃO)
(TRAÇÃO)