Calcule para utilizando Euler com . Compare seus resultados com os valores exatos de nos pontos , sabendo que =
Passo 1
Temos essa EDO para analisar:
Onde:
e . E queremos .
Aqui vamos usar Euler de passo . Vamos montar uma tabelinha com os :
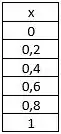
Logo, pela tabela, podemos encontrar uma relação entre . Percebemos que podemos escrever o seguinte:
Isso, porque os valores de são apenas múltiplos de .
Lembramos da fórmula de recorrência:
Nesse caso temos:
Passo 2
A fórmula de recorrência fica:
Substituindo :
Daí ficamos com:
E, aplicando sucessivamente a recorrência para os outros valores de , vamos obter:
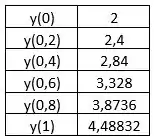
Agora, vamos comparar com os valores reais da função = :
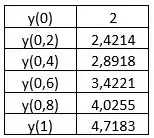
Logo o calculado é . Veja que os valores Método de Euler crescem mais devagar que os reais
Resposta
Exercícios de Livros Relacionados
Utilize o método de Euler para calcular as três primeiras aproximações do problema de valor inicial dado para o tamanho do incremento especificado. Calcule a solução exata e estude a precisão de suas
Utilize o método de Euler com d x = 0,2 para estimar y ( 2 ) se y ' = y x e y 1 = 2 . Qual o valor exato de y 2 .
Use o método de Euler com d x = 1 3 para estimar y ( 2 ) se y ' = xs e ny e y 0 = 1 . Qual é o valor exato de y ( 2 ) ?
Mostre que a solução do problema de valor inicial y ' = x + y , y x 0 = y 0 é y =- 1 - x + 1 + x 0 + y 0 e x - x 0
Use o método de Euler com d x = 0,5 para estimar y ( 5 ) se y ' = y 2 x e y 1 = - 1 . Qual é o valor exato de y ( 5 ) ?