Considere o PVI:
Encontre a solução aproximada usando o método de Euler com e , considerando
Passo 1
Aqui vamos usar Euler com as seguintes configurações
e
Passo 2
A fórmula de recorrência fica:
Para :
Daí:
E sucessivamente obtemos:
Passo 3
Para
Daí:
E sucessivamente, obtemos:
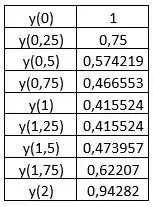
Veja que obtemos uma diferença bastante significativa diminuindo o passo.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Utilize o método de Euler para calcular as três primeiras aproximações do problema de valor inicial dado para o tamanho do incremento especificado. Calcule a solução exata e estude a precisão de suas
Utilize o método de Euler com d x = 0,2 para estimar y ( 2 ) se y ' = y x e y 1 = 2 . Qual o valor exato de y 2 .
Use o método de Euler com d x = 1 3 para estimar y ( 2 ) se y ' = xs e ny e y 0 = 1 . Qual é o valor exato de y ( 2 ) ?
Mostre que a solução do problema de valor inicial y ' = x + y , y x 0 = y 0 é y =- 1 - x + 1 + x 0 + y 0 e x - x 0
Use o método de Euler com d x = 0,5 para estimar y ( 5 ) se y ' = y 2 x e y 1 = - 1 . Qual é o valor exato de y ( 5 ) ?