(Adaptada) Uma câmara de ar frio é proposta para o resfriamento de esferas de aço de rolamento com diâmetro e temperatura inicial . O ar na câmara é mantido a por meio de um sistema de refrigeração e as esferas de aço passam através da câmara em uma esteira transportadora. A produção ótima de rolamentos exige que da energia térmica inicial contida na esfera acima de sejam removidas. Efeitos de radiação pode ser desprezados e o coeficiente de transferência de calor por convecção dentro da câmara é de .
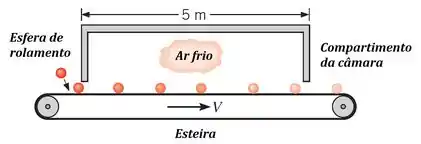
Calcule o tempo de resistência das bolas no interior da câmara.
Estime a velocidade da esteira transportadora, a fim de atender à exigência de operação.
As seguintes propriedades podem ser usadas para o aço: , e .
Passo 1
Calcule o tempo de resistência das bolas no interior da câmara.
As esferas individualmente são como mostrado abaixo:
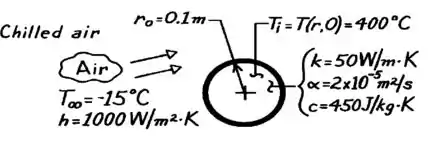
A gente vai analisar uma única esfera logo no começo do equipamento. Então, bora ver se a gente pode usar o Método dos Parâmetros Concentrados nesse problema pelo número de Biot:
O comprimento característico () pela razão entre volume e área da esfera é calculado por:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método dos parâmetros concentrados valer ^^
Assim:
É, não adiantou! Como , a gente não pode usar o Método dos Parâmetros Concentrados! Então, a gente precisa do Método dos Efeitos Espaciais!
Passo 2
Para o caso das esferas sólidas, a gente tem que:
O enunciado afirma que aquelas esferas cuja razão seja de serão removidas, então esse será o critério pra saber quanto tempo elas ficarão lá dentro! Sendo assim:
Pela tabela, conseguimos encontrar as constantes e ! Mas aqui você tem que ter muito cuidado! No finalzinho da tabela com as constantes, tem escrito como que o número de Biot deve ser calculado!
A gente já calculou o número de Biot pra saber se poderíamos usar o Método dos Parâmetros Concentrados. Pra isso, a gente pode escolher como calcular. Mas pra usar a tabela, o número de Biot deve ser calculado da seguinte forma:
Com esse valor de , a gente não precisa interpolar! Temos direto da tabela que:
Substituindo na equação as constantes, a gente fica com:
Passo 3
Além disso, a temperatura adimensional no centro do sólido () é dada por:
Vemos que dá uma indeterminação , logo podemos aplicar o teorema de L’Hospital, derivando numerador e denominador pra tirar novamente o limite:
Em que:
Assim, o número de Fourier () será:
Logo:
Passo 4
Substituindo na equação as constantes e o valor de , a gente fica com:
Isso equivale a aproximadamente !
Passo 5
Estime a velocidade da esteira transportadora, a fim de atender à exigência de operação.
Como a esteira tem de comprimento, como indicado na figura, e o tempo necessário para a esfera ficar no sistema é de , esperamos que a velocidade da esteira seja: