Sistemas de armazenamento de energia térmica em geral envolvem um leito de esferas sólidas, através do qual um gás quente escoa se o sistema está sendo carregado ou um gás frio se o sistema está sendo descarregado. No processo de carregamento, o calor transferido do gás quente aumenta a energia térmica armazenada dentro das esferas frias; durante a descarga, a energia diminui conforme o calor é transferido das esferas aquecidas para o gás refrigerante.
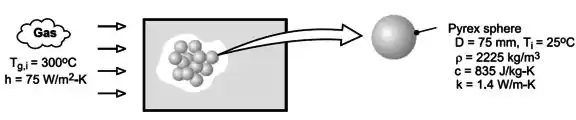
Considere o leito com esferas de pirex (, e ) de 75 mm de diâmetro e o processo de carregamento, para o qual o gás entra na unidade de armazenamento à temperatura de .
Se a temperatura inicial das esferas é de e o coeficiente de convecção é , quanto tempo levará a esfera próxima à entrada do sistema para acumular 90% da máxima energia térmica possível?
Qual a temperatura no centro da esfera?
Passo 1
Se a temperatura inicial das esferas é de e o coeficiente de convecção é , quanto tempo levará a esfera próxima à entrada do sistema para acumular 90% da máxima energia térmica possível?
A situação proposta pode ser ilustrada de maneira simplificada da seguinte forma:
A gente vai analisar uma única esfera logo no começo do equipamento. Então, bora ver se a gente pode usar o Método da Capacidade Concentrada nesse problema pelo número de Biot:
O comprimento característico () pela razão entre volume e área da esfera é calculado por:
Pela distância que corresponde a maior diferença de temperatura, a gente tem que:
Como o fica menor usando a primeira opção, bora usar ele, porque assim fica mais fácil da aproximação do método da capacidade concentrada valer ^^
Assim:
É, não adiantou! Como , a gente não pode usar o Método da Capacidade Concentrada! Então, a gente precisa do Método dos Efeitos Espaciais!
Passo 2
Para o caso de uma esfera, a razão entre as quantidades de calor é dada por:
O enunciado nos pede uma razão de , logo podemos escrever que:
Pela tabela, conseguimos encontrar as constantes e ! Mas aqui você tem que ter muito cuidado! No finalzinho da tabela com as constantes, tem escrito como que o número de Biot deve ser calculado!
A gente já calculou o número de Biot pra saber se poderíamos usar o Método da Capacidade Concentrada. Pra isso, a gente pode escolher como calcular. Mas pra usar a tabela, o número de Biot deve ser calculado da seguinte forma:
Com esse valor de , a gente não precisa interpolar! Temos direto da tabela que:
Substituindo na equação as constantes, a gente fica com:
Passo 3
Além disso, a temperatura adimensional no centro do sólido () é dada por:
Vemos que dá uma indeterminação , logo podemos aplicar o teorema de L’Hospital, derivando numerador e denominador pra tirar novamente o limite:
Em que:
A difusividade térmica () é dada por:
Assim, o número de Fourier () será:
Logo:
Passo 4
Substituindo na equação as constantes e o valor de , a gente fica com:
Isso equivale a aproximadamente !
Passo 5
Qual a temperatura no centro da esfera?
A gente sabe que a temperatura adimensional da esfera é dada por:
Então, avaliando a expressão no centro (), a gente cai no que já achamos antes pelo limite da expressão:
Com as constantes, achamos que:
Logo, pela definição de temperatura adimensional, a gente fica com:
Logo: