Inicia-se a aplicação de um revestimento plástico em painéis de madeira pela deposição de polímero fundido sobre o painel e o posterior resfriamento da superfície do polímero ao submetê-la a uma corrente de ar de .

Como uma primeira aproximação, o calor de reação associado à solidificação do polímero pode ser desprezado e a interface polímero/madeira pode ser considerada adiabática.

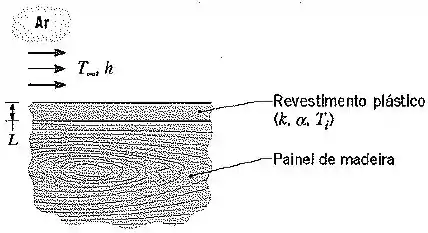
Sendo a espessura do revestimento e ele estando a uma temperatura inicial de , quanto tempo é necessário para a superfície atingir a temperatura segura para o toque de , se o coeficiente de transferência de calor por convecção for ?

Qual é o valor correspondente da temperatura na interface?

A condutividade térmica e a difusividade térmica do plástico são e , respectivamente.

Pelo Método dos Efeitos Espaciais, a temperatura adimensional é dada por:

Onde:

O nosso trabalho agora é encontrar os valores de e . Pra isso, vamos precisar de uma tabela (que provavelmente está no final do seu livro).

Pela Tabela, vemos que o valor de Biot que calculamos está entre dois valores tabela:

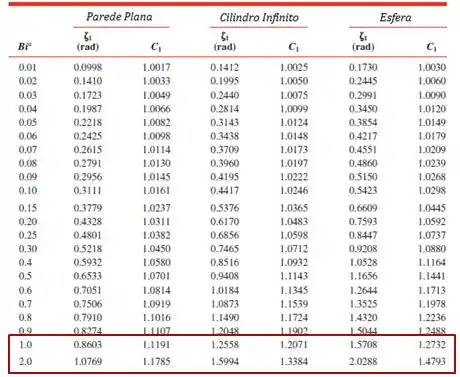
Pra encontrarmos os valores dos parâmetros que precisamos, vamos fazer uma interpolação linear aqui, beleza?

Essa interpolação pode ser feita direto na sua calculadora científica, mas se você for mais hardcore, podemos calcular os parâmetros no braço mesmo:

Utilizando os valores da tabela, encontraremos:

Voltando à equação da temperatura adimensional e substituindo os valores dos parâmetros que acabamos de calcular:

Onde:

Logo:

Sendo , reorganizando a equação acima, o número de Fourier será dado por:

Por definição, o número de Fourier é dado por:

Assim, o tempo necessário para que se atinja a temperatura de será:

Para encontrar a temperatura na interface, basta utilizar a equação para a temperatura adimensional, considerando . Dessa forma:

Sendo :

Substituindo os valores das temperaturas: