Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método dos Efeitos Espaciais

Ver Teoria
Exercício 712345689

Enunciado

Um armazenamento de energia térmica consiste em um grande canal retangular no qual é bem isolado em sua superfície externa e engloba camadas alternadas de material de armazenagem e canal de escoamento.

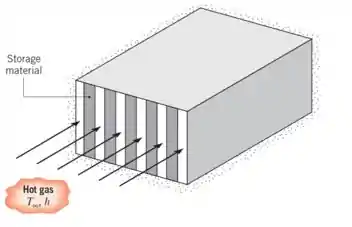
Cada camada do material de armazenamento é uma placa de alvenaria ( ρ = 1900   k g . m - 3 , c p =   800   J . k g - 1 . K - 1 e k   = 0,70   W . m - 1 . K - 1 ) de largura W =   0,05   m , a qual está a uma temperatura de 25 o C . Considere condições para as quais a unidade de armazenamento é carregada pela passagem de um gás quente através dos canais. A temperatura do gás e o coeficiente de convecção são considerados valores constantes de T ∞ = 600 o C e h = 100   W . m - 2 . K - 1 em todo o canal.

  1. Quanto tempo levará para atingir 75% da energia máxima possível armazenada?
  2. Quais são as temperaturas máxima e mínima da alvenaria nesse instante?

Passo 1

a) A situação exposta pelo enunciado pode ser vista da seguinte forma:

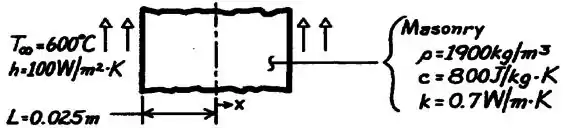
A primeira coisa que temos que fazer é calcular o número de Biot, então bora lá:

B i = h . L c k             →             B i = h . W 2 . k

Substituindo os dados:

B i = 100   W . m - 2 . K - 1 . 0,05   m 2 . 0,70   W . m - 1 . K - 1

B i = ~ 3,6

Como o B i > 0,1 , a gente não pode desprezar os gradientes de temperatura no interior do sólido e precisamos usar o Método dos Efeitos Espaciais!

Passo 2

Sabemos que a energia máxima (no instante t = 0   s ) a ser trocada é dada por:

Q 0 = ρ . V . c p . T i - T ∞

Para o caso de paredes planas, a gente pode escrever:

Q Q 0 = 1 - s e n ζ 1 ζ 1 . θ *

Temos que encontrar o tempo no qual a razão equivale a:

Q Q 0 = 0,75

Ou seja:

s e n ζ 1 ζ 1 . θ * = 0,25

Substituindo a expressão da temperatura adimensional ( θ * ), a gente fica com:

s e n ζ 1 ζ 1 . C 1 . exp ⁡ - ζ 1 2 . F o = 0,25

Em que:

F o = α . t L c 2

A difusividade térmica ( α ) é dada por:

α = k ρ . c p             →             α = 0,70   W . m - 1 . K - 1 1900   k g . m - 3 . 800   J . k g - 1 . K - 1             →             α = 4,61   x   10 - 7   m 2 s

Assim, o número de Fourier ( F o ) será:

F o = 4,61   x   10 - 7   m 2 . s - 1 . t 0,025   m 2

F o = 7,37   x   10 - 4   s - 1 . t

Passo 3

Pela tabela de valores de ζ 1 e C 1 , a gente pode fazer uma interpolação para encontrar esses valores para o caso em que B i = 3,6 ! Bora lá então:

  • Cálculo de ζ 1 :

    • 3,6 - 3,0 4,0 - 3,0 = ζ 1 - 1,1925 1,2646 - 1,1925

    ζ 1 = 1,2358   r a d

  • Cálculo de C 1 :

3,6 - 3,0 4,0 - 3,0 = C 1 - 1,2102 1,2287 - 1,2102

C 1 = 1,2213

Passo 4

Substituindo a expressão para o número de Fourier e os valores das constantes, a gente tem que:

s e n 1,2358 1,2358 . 1,2213 . exp ⁡ - 1,2358 2 . 7,37   x   10 - 4   s - 1 . t = 0,25

Assim:

exp ⁡ - ( 1,1255   x   10 - 3 ) . t = 0,2679

t = ~ 1170   s

Isso equivale a aproximadamente 19,5   m i n .

Passo 5

b) Agora a gente precisa determinar as temperaturas máxima e mínima no sólido! O sólido está esquentando, devido à convecção com o fluido pela superfície. Então, num dado instante, a gente espera que a temperatura máxima seja na parede e a mínima no centro.

Então a gente precisa calcular a temperatura em duas regiões: em x * = 0 (no centro) e em x * = 1 (na parede)! A temperatura adimensional no caso de parede plana é aproximadamente:

θ * = ~ C 1 . exp ⁡ - ζ 1 2 . F o . cos ⁡ ζ 1 . x *

Substituindo as constantes:

θ * = ~ 1,2213 . exp ⁡ - 1,2358 2 . ( 0,8623 ) . cos ⁡ 1,2358 . x *

θ * = ~ 0,327 . cos ⁡ 1,2358 . x *

Passo 6

A temperatura mínima ( x * = 0 ) será:

θ x * = 0 * = ~ 0,327 . cos ⁡ 1,2358 . ( 0 )

T x * = 0 - T ∞ T i - T ∞ = ~ 0,327

Isolando a temperatura de interesse:

T x * = 0 = 873   K + 0,327 . 298 - 873   K  

T x * = 0 = 684,8   K

A temperatura máxima ( x * = 1 ) será:

θ x * = 1 * = ~ 0,327 . cos ⁡ 1,2358 . 1

T x * = 1 - T ∞ T i - T ∞ = ~ 0,108

Isolando a temperatura de interesse:

T x * = 1 = 873   K + 0,108 . 298 - 873   K  

T x * = 1 = 811,2   K

Resposta

  1. t = ~ 1170   s
  2. T x * = 0 = 684,8   K   m í n   e   T x * = 1 = 811,2   K   m á x

Exercícios de Livros Relacionados

Repita o Prob 4-126 para geometrias de ferro fundido ( k=50W / m . ° Ceα=1,57 x 10 - 5 m ² / s ² ).
55. Durante a operação transiente, o ejetor de um motor de foguete, feito em aço, não deve exceder uma temperatura máxima de operação de 1500 K quando exposto a gases de combustão caracterizados por u
57. Em um processo de têmpera, uma lâmina de vidro que se encontra inicialmente a uma temperatura uniforme Ti é resfriada pela redução súbita da temperatura em ambas as superfícies para Ts. A lâmina t
Um longo bastão de plástico com 30 mm de diâmetro (k = 0,3 W/(m · K) e ρcp = 1040 kJ/(m3 · K) é aquecido uniformemente em uma estufa como preparação para uma operação de prensagem. Para obtenção de me
A condutividade térmica de um sólido cuja densidade e calor específico são conhecidos pode ser determinada a partir da relaçãok = α ρ c P após avaliação da difusividade térmica α . Considere uma barra