Um longo bastão de plástico com de diâmetro e é aquecido uniformemente em uma estufa como preparação para uma operação de prensagem. Para obtenção de melhores resultados, a temperatura no bastão não deve ser inferior a .
Até que temperatura uniforme o bastão deve ser aquecido na estufa se, para o pior dos casos, o bastão repousa sobre uma esteira transportadora por antes da prensagem, permanecendo exposto a um resfriamento por convecção ao ar ambiente a , com um coeficiente convectivo de ?
Uma outra condição para a obtenção de bons resultados é a diferença entre as temperaturas máxima e mínima no bastão, que não deve exceder .
Essa condição é satisfeita e, se não, o que você poderia fazer para satisfazê-la?
Passo 1
Logo de cara vamos calcular o número de Biot para o cilindro:
Onde:
Substituindo os valores:
Logo, vamos utilizar o Método dos Efeitos Espaciais pra resolver esse problema.
Passo 2
A temperatura adimensional para o caso do cilindro é dada por:
Vamos agora determinar os valores dos parâmetros que estão faltando na equação.
Para pegar os valores de e da tabela, temos que calcular Biot da seguinte forma:
Como já temos o valor do número de Biot, podemos pegar e direto da tabela. Dessa forma:
Além disso, como o problema já nos deu o tempo que o bastão fica na estufa, podemos calcular o número de Fourier :
Substituindo os valores:
A função de Bessel de primeira ordem é dada em uma tabela a partir dos valores de e . Dado que estamos preocupados com a temperatura na superfície, . Como já calculamos o valor de , teremos:
Na tabela, vemos que esse valor está entre e .
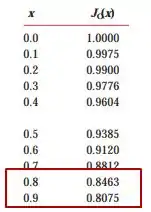
Fazendo uma interpolação linear, encontramos que .
Finalmente, substituindo todos os valores na expressão da temperatura adimensional:
Passo 3
Pra calcular a temperatura inicial do bastão, basta utilizar a definição da temperatura adimensional :
Substituindo os valores:
Passo 4
Vamos utilizar agora a condição de que a diferença entre as temperaturas máxima e mínima no bastão, que não deve exceder .
A máxima temperatura no bastão será a sua temperatura no eixo central. Dessa forma, é mais jogo usarmos essa expressão da temperatura adimensional:
Substituindo os valores:
Assim, a diferença entre as temperaturas máxima e mínima será:
Assim, a condição não é atingida.
Resposta
A condição de que a diferença entre as temperaturas máxima e mínima no bastão, que não deve exceder não é atingida.