Como parte de um processo de tratamento térmico, bastões de aço inoxidável 304 com de diâmetro são resfriados a partir de um temperatura inicial de pela sua suspensão em um banho de óleo a .
Se um coeficiente de transferência de calor por convecção de for mantido pela circulação do óleo, quanto tempo demora para o eixo central dos bastões atingir uma temperatura de , quando então ele é retirado do banho?
Se 10 bastões de comprimento forem processados por hora, qual é a taxa nominal na qual energia deve ser retirada do banho (a carga de resfriamento)?
Passo 1
Logo de cara, precisamos calcular o número de Biot pra saber se podemos usar o Método dos Parâmetros Concentrados, mas o problema não nos deu todos os dados. E agora?!
Nesse caso, a gente costuma buscar os dados no final do livro (provavelmente em um dos apêndices). De acordo com a tabela A.1 do Incropera, para o aço inoxidável 304, temos:
Dessa forma:
Onde:
Substituindo dos valores:
Dessa forma, vamos usar o Método dos Efeitos Espaciais.
Passo 2
Um detalhe importante aqui é que, para pegarmos os valores tabelados de e temos que calcular Biot da seguinte forma:
Olhando na tabela:
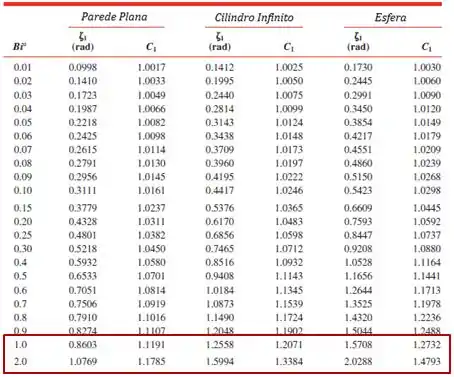
Fazendo uma interpolação linear:
Como estamos preocupados com a região central do bastão, , logo:
Sendo , , e :
Passo 3
Reorganizando os termos dessa equação:
Utilizando a definição do número de Fourier:
Substituindo os valores:
Passo 4
A quantidade de calor transferida é dada por:
Onde é a quantidade de calor transferida inicialmente, dada por:
Onde:
Substituindo todos os valores:
Passo 5
No entanto, essa é a energia transferida por cada bastão.
A taxa total nominal de energia transferida pelos 10 bastões será dada por: