Num arranjo experimental os pontos e funcionam como fontes de luz idênticas emitindo em fase com comprimentos de onda .
A distância entre e pode ser variada, e encontra-se a uma distância do anteparo.
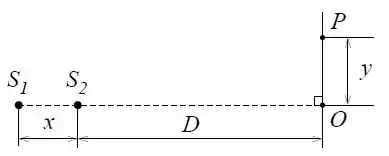
- Obtenha a expressão para a diferença de fase entre as ondas no ponto . (obs: NÃO faça nenhuma aproximação).
- Para que valores de obtém-se interferência destrutiva para (ponto )?
- Se apenas um dos ou estiver presente a intensidade observada no ponto do anteparo é aproximadamente constante e igual a para e pequenos (as amplitudes dos campos elétricos devidos às fontes em são aproximadamente iguais: ).
Deduza a expressão da intensidade resultante observada no ponto como função apenas de e .
Passo 1
Letra a)
A diferença de fase entre as ondas no ponto vai ser resultado da diferença no percurso percorrido pelas ondas emitidas por e por . Podemos visualizá-las no desenho
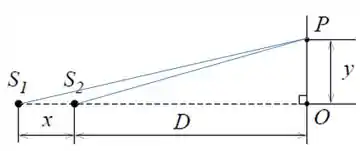
Pelo desenho, podemos encontrar ambas as distâncias percorridas pelos triângulos retângulos desenhados e ver a diferença entre elas.
A distância entre a fonte e o ponto é:
Já entre e é:
Logo, a diferença de caminho é
Passo 2
Com a diferença de caminho calculada, precisamos passar ela para a diferença de fase. Para isso, sabemos que, em múltiplos do comprimento de onda, a diferença de fase vai ser:
Fazendo uma regra de três, temos que a diferença de fase de comprimento de onda é , o de vai ser:
Passo 3
Letra b)
Para , a diferença de fase fica:
O que podia também ser visto pelo gráfico, que quando , o ponto está na reta que liga e e a diferença de percurso das ondas eletromagnéticas fica sendo a distância entre as fontes.
Para que a interferência seja destrutiva, precisamos que a diferença de fase seja equivalente a meio comprimento de onda, ou seja:
Onde corresponde a uma diferença de fase de comprimentos de onda, que mantém as ondas em fase, e corresponde a uma diferença de fase de meio comprimento de onda.
Igualando na equação acima:
Assim, os valores de para os quais se obtêm interferência destrutiva são
Passo 4
Letra c)
Os campos elétricos das respectivas fontes no ponto vão ser:
Como , o campo elétrico resultante no ponto é
Agora, podemos usar uma fórmula trigonométrica para melhorar isso. A fórmula é:
Que era uma fórmula do formulário original da prova! Isso nos dá:
Passo 5
Com o campo elétrico resultante, nós podemos encontrar a intensidade resultante!
A intensidade é diretamente proporcional à média temporal do campo elétrico. No caso da intensidade original (com apenas uma fonte)
Não precisa se preocupar muito quais a constante , porque vamos ver que ela vai “cortar” depois. Além disso, também era uma fórmula dada na prova, não se preocupe!
Temos (novamente, outra fórmula que vinha do formulário e por isso não se preocupe em decorá-la)
Logo:
Façamos o raciocínio para o campo elétrico resultante .
Vamos agora tirar da média temporal tudo que permanece constante ao longo do tempo.
A média do coseno ao quadrado continua valendo!
O que nos dá
Resposta
Letra a)
Letra b)
Letra c)