Duas fontes emitem campos elétricos na mesma direção e de mesma frequência com amplitudes iguais a .
Os campos interferem num ponto em que a diferença de fase entre eles é de .
A amplitude resultante será (dica: use fasor):
Passo 1
O problema nos dá a amplitude dos campos elétricos e a diferença de fase entre eles , e nos pede para calcular o campo elétrico resultante no ponto .
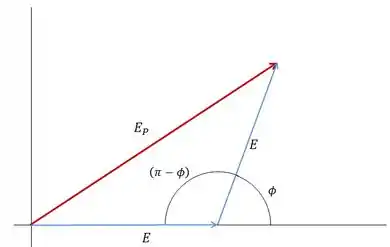
De acordo com os dados, o diagrama de fasores pode ser dado por:
Passo 2
Analisando o diagrama de fasores, a amplitude do campo elétrico resultante é calculado a partir da Lei dos Cossenos para o triângulo formado:
Onde:
;
;
;
Logo:
Resposta
Letra (e):
Exercícios de Livros Relacionados
Determine a resultante de duas ondas cujos campos elétricos em uma dada posição variam com o tempo como se segue: 2 A 0 =E 1 →2,0s e nw t i ^ e 3 A 0 =E 2 →3,0s e n( w t + 3 2 π ) i ^ .
Na difração de fenda simples de Fraunhofer, o padrão de intensidade (Figura 33-11) consiste em um máximo central largo com uma sequência de máximos secundários de cada lada do máximo central. A intens
Três fendas, cada uma separada da fenda ao lado por 60,0μ m , são iluminadas no máximo central de intensidade por uma fonte de luz coerente com comprimento de onda igual a 550n m . As fendas são extre
Luz monocromática incide em uma lâmina que tem quatro fendas longas, estreitas e igualmente espaçadas por uma distância d . (a) Mostre que as posições dos mínimos de interferência em um anteparo a uma
Luz monocromática incide em uma lâmina que contém uma fenda longa e estreita (Figura 33-45). Seja I 0 a intensidade no máximo central do padrão de difração em um anteparo distante, e seja I a intensid