– Obtenha o campo elétrico resultante da soma vetorial dos seguintes campos elétricos em uma interferência produzida por um dispositivo com três fendas:
Passo 1
Para obtermos o campo elétrico resultante, precisamos construir um diagrama de fasores para enxergar o resultado final da soma.
Para isso, vamos observar os ângulos relativos entre , e .
A diferença de fase entre e é de e, por isso, o ângulo entre seus fasores vai ser que corresponde a um ângulo:
Já entre e temos , e o ângulo vai ser:
Isso corresponde a dizer que e serão paralelos mas com sentidos opostos. Além disso, o tamanho dos fasores seria igual à amplitude dos campos elétricos.
O diagrama fica (os tamanhos não estão em escala):
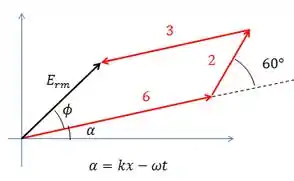
A expressão de cada campo elétrico é a projeção do seu respectivo fasor ao longo do eixo vertical (que é a sua amplitude multiplicada pelo seno do seu ângulo).
Passo 2
Agora, o que podemos fazer é somar as componentes ao longo do eixo obtido quando prolongamos o fasor de . Isso facilita muito o nosso trabalho!
Com isso, ficamos com:
Podemos então achar a amplitude de :
Passo 3
Agora, precisamos achar o ângulo .
Para isso, temos duas relações que podemos usar com uma calculadora!
Vamos usar a primeira.
A expressão final do campo elétrico resultante vai ser a projeção do fasor de no eixo vertical.