Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método dos Fasores

Ver Teoria
Exercício 31245678910111213

Enunciado

Cinco ondas eletromagnéticas senoidais de mesma amplitude incidem num detector, cujos campos elétricos, neste ponto, são dados por:

E 1 = E 0 cos ⁡ ω t

E 2 = E 0 cos ⁡ ω t + 45 °

E 3 = E 0 cos ⁡ ω t + 90 °

E 4 = E 0 cos ⁡ ω t + 135 °

E 5 = E 0 cos ⁡ ω t + 180 °

A amplitude do campo elétrico resultante E R no detector é dada por:

  1. 1 + 2 E 0
  2. E 0
  3. E R = 0
  4. 5 E 0
  5. 2 2 E 0
  6. Nenhuma das anteriores

Passo 1

Vamos começar esboçando o diagrama de fasores, em t = 0 , pra essa situação:

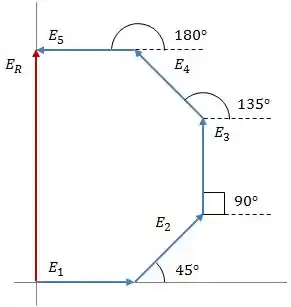
Passo 2

Como o campo elétrico resultante está na vertical, temos apenas que calcular as componentes verticais de cada campo elétrico.

E 1 V = E 0 sen ⁡ 0 ° → E 1 V = 0

E 2 V = E 0 sen ⁡ 45 ° → E 2 V = 2 2 E 0

E 3 V = E 0 sen ⁡ 90 ° → E 3 V = E 0

E 4 V = E 0 sen ⁡ 135 ° → E 4 V = 2 2 E 0

E 5 V = E 0 sen ⁡ 180 ° → E 5 V = 0

Assim, o campo elétrico resultante será:

E R = E 1 V + E 2 V + E 3 V + E 4 V + E 5 V

E R = 2 2 E 0 + E 0 + 2 2 E 0

E R = E 0 + 2 E 0

E R = 1 + 2 E 0

A resposta certa é a letra a .

Resposta

a ) 1 + 2 E 0

Exercícios de Livros Relacionados

Determine a resultante de duas ondas cujos campos elétricos em uma dada posição variam com o tempo como se segue: 2 A 0 =E 1 →2,0s e nw t i ^ e 3 A 0 =E 2 →3,0s e n( w t + 3 2 π ) i ^ .
Na difração de fenda simples de Fraunhofer, o padrão de intensidade (Figura 33-11) consiste em um máximo central largo com uma sequência de máximos secundários de cada lada do máximo central. A intens
Três fendas, cada uma separada da fenda ao lado por 60,0μ m , são iluminadas no máximo central de intensidade por uma fonte de luz coerente com comprimento de onda igual a 550n m . As fendas são extre
Luz monocromática incide em uma lâmina que tem quatro fendas longas, estreitas e igualmente espaçadas por uma distância d . (a) Mostre que as posições dos mínimos de interferência em um anteparo a uma
Luz monocromática incide em uma lâmina que contém uma fenda longa e estreita (Figura 33-45). Seja I 0 a intensidade no máximo central do padrão de difração em um anteparo distante, e seja I a intensid