Obtenha o campo elétrico resultante da soma vetorial dos seguintes campos elétricos em uma interferência produzida por um dispositivo com três fendas:
Passo 1
Queremos calcular a seguinte soma vetorial:
Para calcular a soma vetorial, uma boa dica é desenhar os vetores em um diagrama, lembrando que estamos somando os três vetores dados.
Para facilitar, iremos fazer a seguinte substituição:
Desse modo, podemos montar o seguinte diagrama:
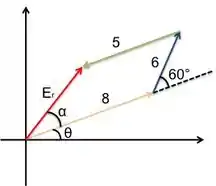
Explicitamente, queremos somar:
Podemos ver no diagrama que estão especificados os vetores dados, assim como o vetor soma .
O campo elétrico resultante da soma será:
Para determinar precisamos recorrer a algumas relações matemáticas, se liga!
Passo 2
Pelo desenho, podemos ver a seguinte relação:
Veja que estamos analisando a soma das componentes de todos os vetores na direção do vetor .
Analisando a outra componente, temos:
Passo 3
Agora que temos o valor das duas componentes, podemos determinar utilizando o teorema de Pitágoras, dá uma olhada!
Substituindo os valores, temos:
Passo 4
Precisamos agora determinar o ângulo , para isso, basta fazer:
O campo elétrico resultante é:
Resposta