Em um experimento de Young, observa-se a intensidade da luz em um anteparo a da fenda dupla. O feixe incidente tem comprimento de onda . Observa-se que, a partir do eixo central, a terceira mancha escura está a uma distância de do centro da figura de interferência.
a) Qual a diferença de caminho ótico entre os raios que chegam no ponto médio dessa terceira mancha escura?
b) Qual é a distância entre as fendas?
Suponha que agora há três fendas, equidistantes de . Faça as questões a seguir literalmente, tomando como conhecido .
c) Escreve a expressão para o campo elétrico total em um ponto na tela, com abertura angular em relação ao eixo central, escrevendo o campo elétrico da primeira fenda (a mais superior) da forma e considerando a diferença de fase pelas fendas subsequentes.
d) Mostre, via método de soma de fasores, que a intensidade da luz em um ponto da tela de observação é dada por , onde .
Passo 1
Fala pessoal, prontos para uma questão de física 4?
Nesse problema vamos brincar com o experimento de Young! A seguir faço um esboço da situação descrita para os itens (a) e (b):
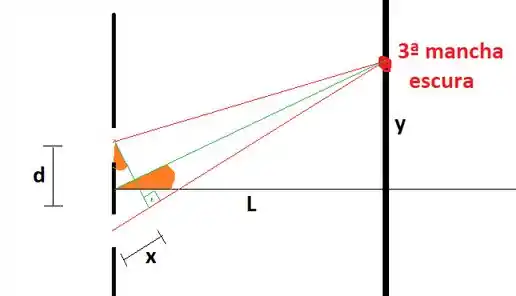
Os raios de luz provenientes das fendas se encontram no ponto marcado que corresponde à terceira mancha escura. A diferença de caminho é representada pela letra . Os demais dados do problema são e .
No item (a) queremos saber a diferença de caminho . Sabemos, no geral, que se a interferência é destrutiva (mancha escura), a diferença de caminho deve corresponder a um múltiplo ímpar de :
A primeira mancha escura ocorre para , a segundo para e a terceira para :
Daí é só substituir :
Portanto, a diferença de caminho é
Passo 2
Para o item (b) temos que olhar para o ângulo pintado em laranja, que chamarei de . Sabemos que a diferença de caminho é dada por
Além disso, usando trigonometria em triângulo retângulo:
Vemos que se trata de um ângulo muito pequeno, de modo que podemos usar a aproximação de ângulos pequenos:
Portanto, usando o resultado do item (a):
Com isso, vemos que a distância entre as fendas é
Passo 3
Agora vamos paras os itens (c) e (d)! Primeiro vamos olhar para esse esboço das três fendas:
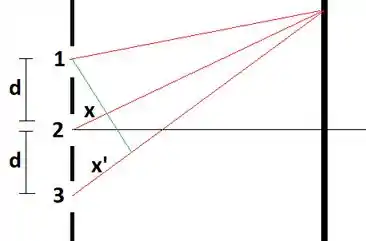
O campo da fenda superior é
Já para as demais fendas teremos:
Nosso trabalho é achar as defasagens e . Para isso, basta lembrar que a defasagem é o número de onda vezes a diferença de caminho:
A diferença de caminho entre o raio 2 e o raio 1 é simplesmente
Já para a diferença :
Portanto,
Com isso, os campos são:
Somando os três campos:
Passo 4
No item (d) temos que fazer a soma desses campos para achar a intensidade que é proporcional ao quadrado do campo. Mas antes de fazer a soma, vamos lembrar que . Assim,
Com isso, podemos escrever:
Fiz isso para simplificar um pouco a expressão e porque nossa resposta deve depender desse !
Para fazer essa soma vamos usar o truque dos fasores no plano complexo. Lembre-se que
Portanto,
Com isso, podemos escrever
Logo,
É mais fácil trabalhar com exponencias do que com funções trigonométricas. Depois de brincar com as exponenciais, basta tomar a parte imaginária!
Passo 5
Vamos olhar para a expressão
Podemos colocar em evidência:
Agora vamos usar que e . Portanto,
Aí você deve lembrar que
Logo,
Portanto,
Ou ainda,
Com isso, temos que
Tomando a parte imaginária:
Passo 6
Para a intensidade, só estamos interessados na amplitude do campo ao quadrado:
Como a amplitude é proporcional ao fator , podemos escrever que
Nessa expressão, corresponde a intensidade do máximo central que ocorrer em , de modo que .
Com isso terminamos o problema!