Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método dos Fasores

Ver Teoria
Exercício 81234567910111213

Enunciado

Origem do Exercício

Em determinado ponto no espaço observa-se que a superposição de 3 ondas planas eletromagnéticas monocromáticas produz um campo elétrico cuja amplitude é:

E t = E 0 cos ⁡ ω t + cos ⁡ ω t + π 3 + cos ⁡ ω t + 2 π 3

Afirmamos então que E t pode ser escrito de maneira mais compacta como E ' cos ⁡ ω ' t + ϕ , onde E ' , ω ' e ϕ é igual a:

Passo 1

Pela fórmula de E t , as ondas planas que se superpõem são:

E 1 t = E 0 cos ⁡ ω t

E 2 t = E 0 cos ⁡ ω t + π 3

E 3 t = E 0 cos ⁡ ω t + 2 π 3

Para resolver um problema onde várias ondas se somam formando uma nova onda, a ferramenta é sempre a mesma: Os super fasores!

Passo 2

Vamos contruir o diagrama fasorial desse sistema.

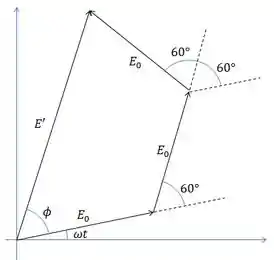
Pelo diagrama fasorial, o ângulo entre E 1 e E 2 é 60 ° enquanto o ângulo entre E 1 e E 3 é igual a 120 ° . Temos também que todos esses fasores têm mesma amplitude E 0 .

Uma forma bem direta de fazer isso é decompor a soma ao longo da direção de E 1 .

Passo 3

Primeiro vamos tentar achar a amplitude E ' .

Decompomos cada fasor ao longo da direção de E 1 e depois ao longo da direção perpendicular a E 1 .

E ' cos ⁡ ϕ = E 0 + E 0 cos ⁡ 60 ° + E 0 cos ⁡ 120 ° = E 0 + E 0 2 - E 0 2 = E 0

E ' sen ⁡ ϕ = E 0 sen ⁡ 60 ° + E 0 sen ⁡ 120 ° = E 0 3 2 + E 0 3 2 = 3 E 0

Pela relação de Pitágoras:

E ' 2 = E ' 2 cos 2 ⁡ ϕ + E ' 2 sen 2 ⁡ ϕ = E 0 2 + 3 E 0 2

E ' 2 = 4 E 0 2 →     E ' = 2 E 0

Agora, vamos achar a constante de fase ϕ . Para isso, podemos achar seu seno e cosseno ou só a sua tangente.

cos ⁡ ϕ = E 0 E ' = 1 2

sen ⁡ ϕ = 3 E 0 E ' = 3 2

tan ⁡ ϕ = 3

O ângulo correspondente é ϕ = 60 ° = π / 3   . Já a constante de tempo ω pelo diagrama é exatamente a mesma dos outros fasores:

ω ' = ω

Resposta

E ' = 2 E 0

ϕ = 60 ° = π 3

ω ' = ω

Juntando tudo:

E t = 2 E 0 cos ⁡ ω t + π 3

Exercícios de Livros Relacionados

Determine a resultante de duas ondas cujos campos elétricos em uma dada posição variam com o tempo como se segue: 2 A 0 =E 1 →2,0s e nw t i ^ e 3 A 0 =E 2 →3,0s e n( w t + 3 2 π ) i ^ .
Na difração de fenda simples de Fraunhofer, o padrão de intensidade (Figura 33-11) consiste em um máximo central largo com uma sequência de máximos secundários de cada lada do máximo central. A intens
Três fendas, cada uma separada da fenda ao lado por 60,0μ m , são iluminadas no máximo central de intensidade por uma fonte de luz coerente com comprimento de onda igual a 550n m . As fendas são extre
Luz monocromática incide em uma lâmina que tem quatro fendas longas, estreitas e igualmente espaçadas por uma distância d . (a) Mostre que as posições dos mínimos de interferência em um anteparo a uma
Luz monocromática incide em uma lâmina que contém uma fenda longa e estreita (Figura 33-45). Seja I 0 a intensidade no máximo central do padrão de difração em um anteparo distante, e seja I a intensid