Seja um sistema de fenda dupla tal que a distância entre as fendas é e a distância até um anteparo é , como mostrado na figura. A partir da esquerda e direção perpendicular à fenda, incide uma onda luminosa de comprimento de onda . Para ângulos não muito grandes, seja a intensidade da luz no anteparo quando apenas uma fenda está aberta.
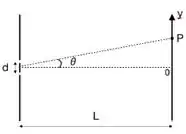
a) Obtenha, pelo método que escolher, a intensidade da luz no anteparo quando as fendas estão abertas, em função do ângulo e em função de .
b) Faça um esboço, em função de , da intensidade da luz no anteparo. Admita que vale a aproximação de pequenos ângulos.
c) Seja , e . Encontre quais são as posições em , entre os máximos de ordem e , para os quais a intensidade é metade da intensidade máxima.
d) Inserindo uma lâmina de vidro com índice de refração e espessura em uma das fendas, de quanto se desloca a posição do máximo central no anteparo?
Passo 1
Eai galerinha, bora resolver mais uma questão de física 4!
Nesse problema vamos analisar o famoso experimento de Young que trata da interferência entre duas fendas. No item (a) o enunciado quer que a gente deduza a expressão para a intensidade da luz no anteparo. Para fazer isso, vamos considerar o desenho:
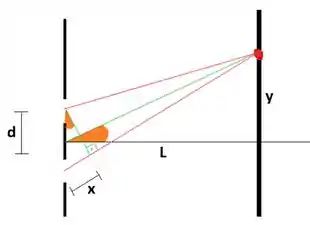
As ondas que passam pelas fendas inferior e superior vão se encontrar no anteparo e daí que vai aparecer a interferência. Vamos chamar fenda inferior de 1 e a superior de 2. Se for a distância percorrida pela onda 1 e a distância percorrida pela onda 2 até atingir o anteparo, temos as seguintes expressões para os campos elétricos de cada onda:
Antes de prosseguir, vou fazer uma pequena digressão:
Somando as duas equações:
Agora vamos definir
Substituindo na equação acima:
Chamando e , achamos
Com isso, achamos
Essa é a expressão para o campo elétrico em algum ponto do anteparo.
Passo 2
Vamos olhar com atenção para o desenho: observe que a diferença de caminho entre os raios é
Além disso, podemos escrever
No desenho, é a distância representada pelo segmento verde entre o ponto médio das fendas e um ponto no anteparo. O ponto no anteparo é determinado pelo ângulo que esse segmento faz com o eixo horizontal.
Com essa definição, temos que
Logo, o campo total fica
O primeiro cosseno representa uma onda que se propaga. Já o segundo cosseno é o termo responsável pela interferência. Como a intensidade é proporcional ao quadrado do campo, podemos escrever
Lembrando que , achamos
Passo 3
No item (b) queremos escrever a intensidade em termos de . Para isso, primeiro escrevemos
Usando a aproximação de ângulos pequenos:
Logo,
Com isso, a expressão da intensidade é dada por
A seguir fazemos um plot dessa função:
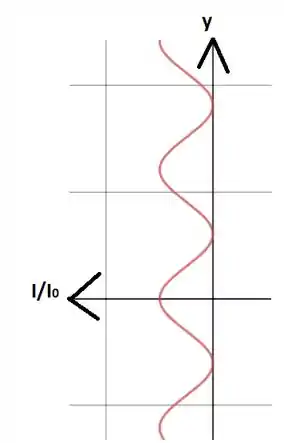
Coloquei o eixo na vertical para ficar mais fácil comparar com o anteparo.
Passo 4
No item (c), queremos achar o ponto entre os máximos de ordem e ordem em que a intensidade seja metade da intensidade máxima . Com isso, podemos escrever
Logo, tirando a raiz quadrada:
Para resolver essa equação, escrevemos
Lembre-se que os ângulos cujo cosseno é são . Aí somamos ou subtraímos múltiplos de para achar os demais ângulos.
Como estamos interessados no ponto entre os máximos de ordem e de ordem , temos que tomar nessa expressão, pois a fase deve estar entre e . Com isso,
Daí é só substituir os valores , e :
Portanto,
Passo 5
Para fechar o problema, vamos para o item (d)!
Na situação descrita nos três primeiros itens, a defasagem é devida apenas a diferença de caminho:
Todavia, no item (d) é colocada uma lâmina de vidro de espessura em uma das fendas, enquanto na outra nada é colocado. Isso vai fazer com que apareça uma defasagem extra:
Usando a expressão para :
No ar temos , já no vidro
Portanto,
Essa defasagem aparece devido a diferença de caminho ótico da onda que percorre o vidro e a onda que não percorre! Considerando as duas contribuições:
Passo 6
Sem a lâmina de vidro, os máximos eram dados por
Como , as posições desses máximos eram
Agora, considerando a lâmina de vidro, temos que os máximos ocorrem em:
Logo,
Considerando máximos de mesma ordem (), a diferença entre as posições no anteparo será
Daí é só substituir os valores:
Portanto, o deslocamento das franjas de máximo de interferência devido à lâmina de vidro foi cerca de .
E com isso nós terminamos o problema 😊!