Achar a equação da parábola que passa pelos pontos , e
Passo 1
Nossa! Não sei nem por onde começar!!

Calma!! Tem um detalhe que ainda não falamos que vai te ajudar muito!!
O detalhe é o seguinte:
- Se a reta diretriz for paralela ao eixo então a equação é
- Se a reta diretriz for paralela ao eixo então a equação é
Passo 2
Então, para acharmos a expressão precisamos identificar à qual eixo a parábola é paralela. Para isso, vamos marcar os pontos no plano e ver qual o jeitão da parábola. Fazendo um esboço bem rápido, temos:
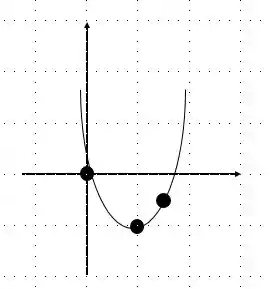
Pela figura nossa parábola possui diretriz paralela ao eixo , então, nossa equação é:
Passo 3
Sabendo disso precisamos substituir os pontos na equação. Substituindo, teremos:
Para
Para
Como
Para
Como ,
Com as expressões e conseguimos achar os valores de e . Resolvendo o sistema a seguir, temos:
Isolando na primeira equação, temos:
Substituindo na segunda equação:
Então,
Chegamos nos valores:
Assim, sabendo que a expressão é , a expressão da nossa parábola fica: