Determine todas as parábolas em posição canônica (vértice na origem e tendo um eixo coordenado como eixo de simetria) que contém o ponto .
Passo 1
Essa parábola pode estar de duas formas diferentes:
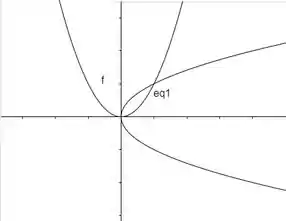
Nas duas formas o vértice ta na origem e o eixo de simetria é um dos eixos coordenados. Além disso, o ponto deve pertencer a essas duas formas, ali no primeiro quadrante (por isso a parábola não pode estar pra esquerda e nem pra baixo).
Passo 2
As duas equações genéricas possíveis pra essas parábolas são:
e
Como elas passam pelo ponto , vamos substituir esse ponto nas duas equações para encontrarmos os parâmetros e .
Substituindo na primeira equação:
Na segunda equação:
Então as duas equações possíveis de parábolas são
Resposta
Exercícios de Livros Relacionados
Ache uma equação da parábola com as propriedades dadas.Vértice ( 0 ,0 ) ; aberta para cima; o comprimento do latus rectum 3 .
Ache uma equação da parábola com as propriedades dadas.Vértice ( 0 ,0 ) ; aberta para esquerda; o comprimento do latus rectum é 6 .
Para a parábola, ache as coordenadas do foco, a equação da diretriz e o comprimento do latus rectum. Faça um esboço da parábola. x 2 = - 16 y
Ache a equação da parábola que tem vértice na origem, eixo no eixo y e passa pelo ponto ( - 2 ,- 4 ) .
Ache uma equação da parábola com as propriedades dadas.Foco ( 0 ,- 2 ) ; diretriz y - 2 = 0 .