Determinar a equação da parábola de vértice , sabendo que é a equação de sua diretriz.
Passo 1
O problema nos dá o vértice e a equação da reta diretriz da parábola, e nós com esses dados devemos determinar a equação desta parábola. Mas, como farei isso, não vimos nada assim!!

Calma!! Vamos por partes!!
Passo 2
Analisando o vértice sabemos que não estamos nem no caso 1 e nem no caso 2, porque nesses dois casos o e temos que . Assim, estamos no caso de uma translação. Além disso, sabemos que a reta diretriz é , isso nos indica que a nossa parábola é da seguinte maneira:
Assim, sabemos que a forma geral da nossa parábola, será:
Passo 3
Para determinar nossa parábola, precisamos então determinar os valoresde e . Para isso, vamos fazer o inverso do que vínhamos fazendo, ou seja, sabemos que no sistema o vértice é e sabemos que no vale .
Assim, teremos:
Substituindo em :
Substituindo em :
Portanto, chegamos na seguinte expressão:
Mas, e quanto vale?
Para achar fica mais fácil fazermos um esboço da parábola.
Passo 4
Fazendo um esboço obtemos a seguinte figura:
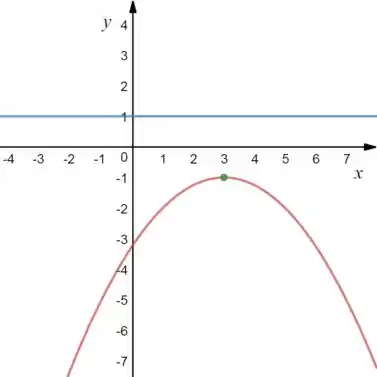
Pela figura temos que:
Que é a distância do nosso vértice em verde pra reta diretriz em azul!
Então !
Eu sei que deve ser um valor negativo, pois a parábola está nos !
Assim, já que achamos o valor de , falta colocar na expressão:
Substituindo:
Prontinho, chegamos na nossa resposta!!