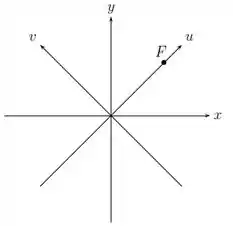
Uma parábola tem vértice na origem e foco . Seja o sistema de coordenadas obtido do sistema por uma rotação anti-horária de .
a) Escreva a equação dessa parábola no sistema .
b) Escreva a equação dessa parábola no sistema .
Passo 1
a) O parâmetro geométrico dessa parábola é dado pela distância entre seu foco e seu vértice, ou seja:
O eixo de simetria da parábola vai ser o eixo , logo:
Passo 2
b) A relação entre os dois sistemas de coordenadas é dada por
Logo, a equação transformada para o sistema fica assim
Resposta
a)
b)
Exercícios de Livros Relacionados
Ache uma equação da parábola com as propriedades dadas.Vértice ( 0 ,0 ) ; aberta para cima; o comprimento do latus rectum 3 .
Ache uma equação da parábola com as propriedades dadas.Vértice ( 0 ,0 ) ; aberta para esquerda; o comprimento do latus rectum é 6 .
Para a parábola, ache as coordenadas do foco, a equação da diretriz e o comprimento do latus rectum. Faça um esboço da parábola. x 2 = - 16 y
Ache a equação da parábola que tem vértice na origem, eixo no eixo y e passa pelo ponto ( - 2 ,- 4 ) .
Ache uma equação da parábola com as propriedades dadas.Foco ( 0 ,- 2 ) ; diretriz y - 2 = 0 .