Determinar a equação da parábola de foco em , sendo a equação da diretriz.
Passo 1
Temos um exerc´ício muito parecido com o anterior!! Mas, agora, não temos mais o vértice, mas o foco. Assim, com o foco e a diretriz devemos determinar a equação da parábola.
Bora começar, então?

Passo 2
Primeiro, devemos ver em qual dos três casos estamos!! Como nenhuma das coordenadas de é zero, isso nos indica que estamos no caso , ou seja, translação. Temos, também outra dica importante!! Como sabemos que a reta diretriz é , então, nossa equação da parábola tem o seguinte formato:
Sempre que tivermos dados como esses é bom fazer um esboço para clarear nosso problema!!
Passo 3
Esboçando, temos:
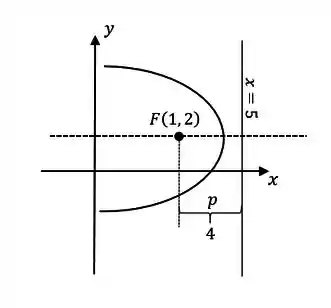
Da figura conseguimos tirar uma primeira informaçãosobre . Devido a concavidade a parábola estar apontando para o lado negativo, isso indica que estamos no caso onde . Assim,
Da figura também conseguimos ver que o vértice da parábola é o ponto médio entre e , logo a coordenada do vértie vale , e a coordenada é a mesma do foco. Assim, temos:
Lá na teoria vimos que quando temos tranlação temos as seguintes relações:
Assim, se temos o vértice em e no sistema temos , temos as relações:
Pronto!! Temos tudo o que precisávamos para completar nossa expressão . Assim, se e :
Chegamos na expressão da nossa parábola!!