O referencial passa pelo referencial a uma velocidade ao longo da direção comum dos eixos e , como na figura abaixo.
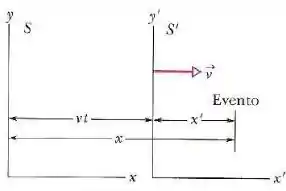
Um observador estacionário no referencial mede um certo intervalo de tempo com seu relógio de pulso. Um observador estacionário no referencial mede o intervalo correspondente .
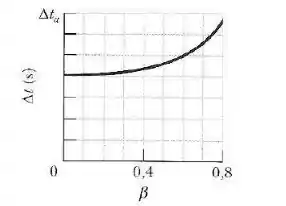
A figura abaixo mostra a variação de com o parâmetro de velocidade no intervalo . A escala do eixo vertical é definida por . Qual é o valor de para ?
Passo 1
A partir da escala dada pelo problema, quando , ou seja, (referencial em repouso), o intervalo de tempo vale .
Logo:
Agora podemos usar a equação de dilatação do tempo para resolver o problema:
Substituindo os valores, teremos:
Resposta
Exercícios de Livros Relacionados
51. As naves da Federação Solar são marcadas com o símbolo da Federação, um círculo, enquanto as naves do Império Denebian são marcadas com o símbolo do Império, uma elipse cujo o eixo maior é 1,40 ve
1 03 . Determine o parâmetro de velocidade para as seguintes velocidades: ( a ) o deslocamento de uma placa tectônica típica ( 2,5c m / a n o ) ; ( b ) a velocidade de deriva dos elétrons em um condut
O píon neutro π 0 tem uma massa de repouso de 135,0 MeV / c2. Esta partícula pode ser criada em uma colisão próton-próton: p + p → p + p + π0. Determine o limiar de energia cinética para a criação de
Use a equação de expansão binomial 1 + x n = 1 + n x + n ( n - 1 ) 2 x 2 + … ≈ 1 + n x , x ≪ 1 para derivar os seguintes resultados para o caso em que v é muito menor que c, e use os resultados quando
Uma espaçonave interestelar viaja da Terra para um sistema estelar a 12 anos-luz de distância (conforme medido no referencial da Terra). A viagem dura 15 anos, conforme medido pelos relógios da nave.