Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Partícula na Caixa – 2D e 3D

Ver Teoria
Exercício 81234567

Enunciado

Numa caixa dimensional onde L x = 4 L y = 2 L z   ,   a função de onda na posição L z , L y 2 ,   L y

é L y × 10 24 , calcule as dimensões da caixa e a energia do elétron considerando que o mesmo está no estado fundamental.

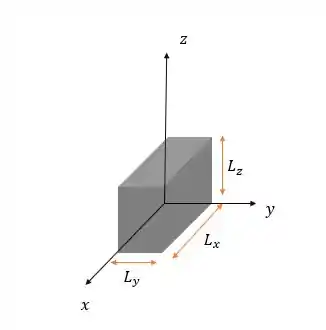
Dado:

Massa do elétron m e = 9,109 × 10 - 31 K g

Passo 1

Precisamos encontrar os lados e nos foi dada a relação entre eles e também o valor da função de onda no ponto assim usaremos essa equação:

ψ x , y = 2 L x . 2 L y . 2 L z . s e n n x π . x L x . s e n n y π . y L y . s e n n y π . z L z

Substituindo na função o ponto L z , L y 2 ,   L y   e também os valores n x = n y = n z = 1 temos:

ψ x , y = 2 L x . 2 L y . 2 L z . s e n π . L z L x . s e n π . L y 2 L y . s e n π . L y L z

Fazendo L x = 4 L y e L z = 2 L y   temos:

ψ x , y = 8 8 . L y 3 . s e n π . 2 L y 4 L y . s e n π . L y 2 L y . s e n π . L y 2 L y

Com o outro lado da equação temos:

L y × 10 24 ,   = 1 L y 3 . s e n π 2 . s e n π 2 . s e n π 2

Como s e n π 2 = 1   :

L y × 10 24 = 1 L y 3

Elevando os dois lados ao quadrado temos:

L y 2 × 10 48 = 1 L y 3

Rearrumando:

L y 5 = 1 10 48

L y = 10 - 48 1 5

L y = 251,2 p m

L x = 4 L y = 1004,8 p m

L z = 2 L y = 502,4 p m

Passo 2

Com três dimensões a energia vai depender de x , y   e z , assim:

E x = n x 2 . h 2 8 m L x 2

E y = n y 2 . h 2 8 m L y 2

E z = n z 2 . h 2 8 m L z 2

A energia total é a soma das energias então:

E x + E y + E z = E t

n x 2 . h 2 8 m L x 2 + n y 2 . h 2 8 m L y 2 + n z 2 . h 2 8 m L z 2 = E t

O enunciado diz que o elétron está no estado fundamental e portanto:

n x = n y = n z = 1

h 2 8 m L x 2 + h 2 8 m L y 2 + h 2 8 m L z 2 = E t

Colocando os termos em evidência temos:

h 2 8 m 1 L x 2 + 1 L y 2 + 1 L z 2 = E t

6,626 × 10 - 34 2 8 × 9,109 × 10 - 31 × 1 1004,8 2 + 1 251,2 2 + 1 502,4 2 × 1 10 - 24 = E t

E t = 1,253 × 10 - 18 J

Resposta

L y = 251,2 p m

L x = 1004,8 p m

L z = 502,4 p m

E t = 1,253 × 10 - 18 J

Exercícios de Livros Relacionados

Um elétron (cuja massa é m ) está confinado em um curral retangular de dimensões L x = L e L y = 2 L . (a) Quantas frequências diferentes o elétron e capaz de emitir ou absorver ao sofrer uma transiçã
Um elétron (cuja massa é m ) está confinado em uma caixa cúbica de dimensões L x = L y = L z (a) Quantas frequências diferentes o elétron é capaz de emitir ou absorver ao sofrer uma transição entre do
Um curral retangular de dimensões L x = L e L y = 2 L contém um elétron. Determine em múltiplos de h 2 / 8 m L 2 , onde m é a massa do elétron, (a) a energia do estado fundamental do elétron; (b) a en
07. Um feixe de elétrons de 2e V incide sobre uma barreira de potencial retangular de 4e V de altura e 10Å Å de espessura. Qual é a probabilidade de transmissão? Qual seria para elétrons de 3e V ?