Num curral dimensional onde , a energia no estado fundamental do elétron é de , encontre as duas dimensões do curral e calcule o valor da função de onda correspondente para as posicões .
Dado:
Massa do elétron
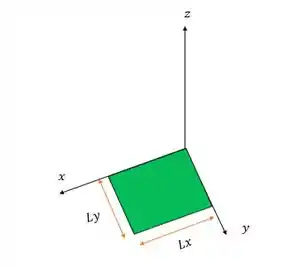
Passo 1
Como temos apenas duas dimensões podemos calcular a nossa energia dependente apenas de e.
A energia total é a soma das duas energias então:
O enunciado diz que o elétron está no estado fundamental e portanto:
Passo 2
Agora que isolamos a energia total podemos trabalhar a equação para encontrarmos os lados da caixa, assim:
Nosso objetivo é encontrar os lados então devemos isolar as dimensões, assim:
E como , temos:
Rearrumando tudo enfim temos:
Substituindo os valores temos:
Passo 3
Encontrados os lados podemos encontrar a nossa função de onda, lembrando que para um curral bidimensional a função de onda pode ser descrita por:
Substituindo na função o ponto temos:
Fazendo e substituindo temos:
Analisando os argumentos dos senos temos o produto de
E = 0 que multiplica toda a função , portanto a função de onda será zero nesse ponto.