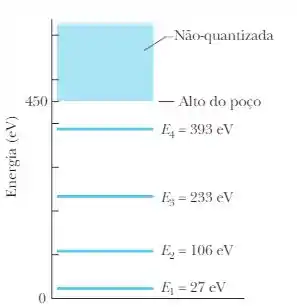
- Calcule a energia necessária para liberar um elétron no estado fundamental preso num poço finito de potencial , use os valores da figura abaixo.
- Esboce os gráficos da densidade de probabilidade dos 3 níveis de menor energia no poço.
Passo 1
a) Primeiro precisamos saber qual é a energia que liberta o elétron do poço, assim pegamos o estado em que se encontra o elétron e fazemos a diferença entre o potencial do posso e a energia do estado, dessa forma:
Passo 2
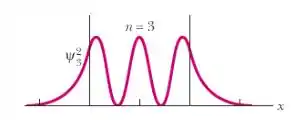
b) Para esboçar os gráficos poderíamos usar as equações, porém é mais simples fazer de forma qualitativa. Podemos pensar que o nível de energia é proprocional ao número de saliências que aparecem no gráfico. Os 3 menores níveis são 1,2 e 3 começaremos por .
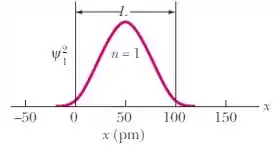
Observe que aparece apenas uma saliência na função dentro do poço.
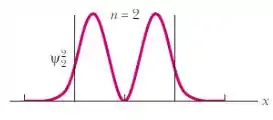
Assim para , devem aparecer duas, como no gráfico abaixo:
E finalmente para :
Resposta
Exercícios de Livros Relacionados
Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 5 do potencial finito do poço quadrado
Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 4 do potencial finito do poço quadrado
Como sugere a figura 39-8, a densidade de probabilidade na região 0xL do poço de potencial finito da figura 39-7 varia senoidalmente, de acordo com a equação ψ 2 x = B s e n 2 k x , onde B é uma const
Como sugere a figura 39-8, a densidade de probabilidade na região xL do poço de potencial finito da figura 39-7 diminui exponencialmente, de acordo com a equação ψ 2 x = C e - 2 k x , onde C é uma con