- Mostre que para região do poço de potencial finito da Fig. 39-7, é uma solução da equação de Schrödinger unidimensional, onde é uma constante e k é um número real positivo.
- Por que razão a solução matemáticamente aceitável do item (a) não é considerada fisicamente admissível?
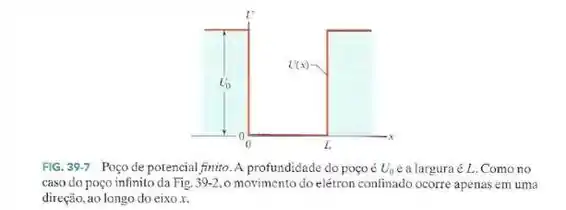
Passo 1
(a) Para o poço de potencial finito a equação de Schrödinger é:
O problema pede para mostrarmos que é uma solução. Para isso basta aplicarmos as derivadas no lado esquerdo da equação e se resultar em zero ela satisfaz. Assim, a primeira derivada da função é:
Aplicando a segunda derivada temos:
Passo 2
Beleza, agora bora substituir na equação o que a gente encontrou. A equação inicial vai ficar com essa cara:
Dividindo os dois lados por :
Isolando o encontramos o valor que satisfaz a equação, dessa forma:
Passo 3
(b) A questão diz pra gente que a região é , o que significa que , fazendo com que a raiz da equação seja positiva e seja real, mas se ele for real então a função que foi dada como solução:
Cresce para valores de positivos de exponencialmente e a integral da densidade de probabilidade não será unitária, então ela é fisicamente impossível.
Resposta
Ei, a resposta está no passo a passo :)