Uma partícula de massa e energia constante , move-se no sentido positivo do eixo na presença de um degrau de potencial.
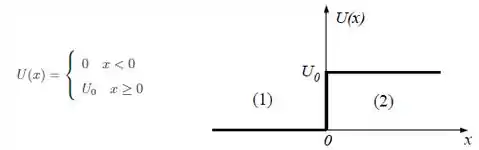
- Escreva a equação de Schrödinger independente do tempo desta partícula para (região ).
- Determine a solução geral da equação de Schrödinger na região para . Qual é a solução fisicamente aceitável para o problema? Justifique.
- Determine a solução geral da equação de Schrödinger na região para . Qual é a solução fisicamente aceitável para o problema? Justifique.
Passo 1
Letra a)
A equação de Schrödinger é
Para a energia potencial é , e assim:
A equação fica:
Passo 2
Letra b)
Para , podemos rearrumar a equação e fazer:
Fazendo , temos:
Cuja solução é uma combinação de senos e cossenos ou, equivalentemente, de duas exponenciais complexas.
No caso das exponenciais complexas é mais fácil enxergar a solução fisicamente aceitável.
Isso é porque a segunda parte, , corresponde a uma partícula se movendo no sentido negativo do eixo , o que vai contra nossa hipótese.
Se a partícula estivesse na região com , ela poderia refletir no degrau e se mover no sentido contrário. Mas além dela estar na região , ela tem .
Por isso, temos que ter .
Passo 3
Letra c)
Para , podemos definir:
E teremos:
Que corresponde a uma exponencial sem expoente complexo.
A medida que , nós temos que , e assim ela não é normalizável.
Por isso, temos que ter para a solução fisicamente aceitável.
Resposta
Letra a)
Letra b)
Solução geral:
Solução fisicamente aceitável:
Letra c)
Solução geral:
Solução fisicamente aceitável: